Packages acting on a conveyor belt

[Like Tony Stark]

Homework Statement

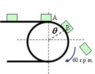
Some packages of mass $0.8 kg$ are deposited on a conveyor belt, whose coefficient of static friction is $0.4$. Determine:
A) The force exerted by the conveyor belt on each package a moment before and after passing by the point $A$.
B) The angular coordinate in point $B$, which is the point where the packages start to slide
C) The angular coordinate when the packages lose contact with the conveyor belt.

Relevant Equations

Newton's equations

A) Before passing by $A$ the forces acting are weight and normal force. Then, after passing by that point you have
(Tangential direction) $W_t-Fr=m.a_t$
(Normal direction) $-N+W_n=m.\omega ^2 .r$
Also, as the packages don't slide, we can say that $a_t=0$
Are these ideas okay?

B) When the packages are about to slide, the static friction is maximum. So you have
$\hat t) W_t-Fr=0$
$W_t=Fr$
$W.sin(\alpha)=\mu N$
From $\hat n$ we know that $N=mg.cos(\alpha)-m.\omega ^2 .r$
So we can replace with that
$mg.sin(\alpha)=\mu (mg.cos(\alpha)-m.\omega ^2 .r)$

The thing is that I don't have $r$ and I don't have $\alpha$.

C) If they lose contact, then $N=0$ and
$\hat n) -N+W_n=m.\omega ^2 r$
$mg.cos(\alpha)=m.\omega ^2 r$
$cos(\alpha)=\frac{\omega ^2 r}{g}$

But I have the same problem that I had in $B$.

 

[haruspex]

For the first part of A, you are asked what force the belt exerts on each package, not what all the forces are on a package. You should answer in terms of the given mass.

For the second part of A, it is not clear what your answers are to the question asked.

For B, yes, you need to know r. Can you solve it algebraically, leaving r as an unknown? There is a trick to this, using the expansion of sin(x+y).

C is awkward. You have overlooked the fact that the package may be already sliding, increasing the angular velocity. I suspect this is more difficult than the questioner intended.

 

[Like Tony Stark]

For the first part of A, you are asked what force the belt exerts on each package, not what all the forces are on a package. You should answer in terms of the given mass.

For the second part of A, it is not clear what your answers are to the question asked.

For B, yes, you need to know r. Can you solve it algebraically, leaving r as an unknown? There is a trick to this, using the expansion of sin(x+y).

C is awkward. You have overlooked the fact that the package may be already sliding, increasing the angular velocity. I suspect this is more difficult than the questioner intended.

So for the first part of A) I should say that
$y) N-W=m.a_y$
$N-W=0$
$N=W$
$N=m.g$
$N=0.8*9.81$
Right?

For the second part of A, I wanted to say that if I want to calculate the forces exerted on the packages, you have to solve something similar to an inclined plane problem:
$\hat t) W_t-Fr=m.a_t$
$W_t-Fr=0$
$W_t=Fr$
$m.g.sin(\alpha)=0.4 N$
Where $N$ is an unknown normal force.
Then
$\hat n) -N+W_n=m.r.\omega ^2$
$-N+m.g.cos(\alpha)=m.r \omega ^2$
$N=mgcos(\alpha)-mr\omega ^2$

And then for C, do you mean that my answer is ok but I should take $\omega$ as a new unknown?

 

[haruspex]

For the second part of A, I wanted to say that if I want to calculate the forces exerted on the packages, you have to solve something similar to an inclined plane problem:

No, you are getting confused. In the second part of A it is still effectively horizontal. Your original equations were fine, but you did not turn them into an answer to the question asked.

for C, do you mean that my answer is ok but I should take ω as a new unknown?

In principle it is known, in the sense that it has a fixed relationship to the angle you are trying to find. Can you figure out what that relationship is? Consider energy (but I have not attempted this myself yet - will when I get a chance).

 

[Like Tony Stark]

No, you are getting confused. In the second part of A it is still effectively horizontal. Your original equations were fine, but you did not turn them into an answer to the question asked.

So the forces acting before and after the point A are the same?

 

[haruspex]

So the forces acting before and after the point A are the same?

No. As I wrote, what you had originally for the second part of A was correct:
after passing by that point you have
(Tangential direction) Wt−Fr=m.at
(Normal direction) −N+Wn=m.ω2.r
Also, as the packages don't slide, we can say that at=0
Are these ideas okay?
All that is wrong is that you did not turn those into an actual answer to the question.
But in post #3 you introduced a variable α for the angle. This is unnecessary since it is vanishingly small.

 

[Like Tony Stark]

No. As I wrote, what you had originally for the second part of A was correct:
after passing by that point you have
(Tangential direction) Wt−Fr=m.at
(Normal direction) −N+Wn=m.ω2.r
Also, as the packages don't slide, we can say that at=0
Are these ideas okay?
All that is wrong is that you did not turn those into an actual answer to the question.
But in post #3 you introduced a variable α for the angle. This is unnecessary since it is vanishingly small.

So if I shouldn't introduce a variable for the angle, I shouldn't do any distinction between $W_t$ and $W_n$. Then, the equations would be
$t) -Fr=m.a_t$
$n) N-P=m.w^2 .r$

 

[haruspex]

So if I shouldn't introduce a variable for the angle, I shouldn't do any distinction between $W_t$ and $W_n$. Then, the equations would be
$t) -Fr=m.a_t$
$n) N-P=m.w^2 .r$

Yes, where a_t=0 (as you wrote in post #1).

I notice you often use P without defining it. Is this standard in your course? I've not come across that convention. It seems to mean mg, right?

 

[Like Tony Stark]

Yes, where a_t=0 (as you wrote in post #1).

I notice you often use P without defining it. Is this standard in your course? I've not come across that convention. It seems to mean mg, right?

Sorry, "P" is for "Peso" ("Weight" in Spanish). I read some physics books written in Spanish and that's why I sometimes use "P" instead of "W". My bad

 

[Like Tony Stark]

In principle it is known, in the sense that it has a fixed relationship to the angle you are trying to find. Can you figure out what that relationship is? Consider energy (but I have not attempted this myself yet - will when I get a chance).

I tried to find the new $\omega$ considering energy. Firstly I said
$\frac{1}{2}mv_1^2+mgh_1=\frac{1}{2} mv_2^2 +mgh_2$

Where $h_1$ is the height of the straight part, $h_2$ the height at which the block falls and the different $v$ are the velocities in those positions. Also, $v_2=\omega_2.r$ and $v_1=\omega_1 .r$

But I realized that there's friction, so the energy won't be conserved. The work done by the friction will be
$W=\frac{1}{2} m.(v_2-v_1)^2$

And now what should I do?

 

[Like Tony Stark]

For B, yes, you need to know r. Can you solve it algebraically, leaving r as an unknown? There is a trick to this, using the expansion of sin(x+y).

I tried something different. I said that $x=sin (\alpha)$ so $\sqrt{1-x^2}=cos(\alpha)$
I had:
$mg.sin(\alpha)=\mu (mg.cos(\alpha)-m\omega ^2 .r)$
Now I have:
$mg.x=\mu (mg.\sqrt{1-x^2}-m\omega^2 .r)$
But I don't know how to solve it, or how to solve it with your method

 

[haruspex]

I tried something different. I said that $x=sin (\alpha)$ so $\sqrt{1-x^2}=cos(\alpha)$
I had:
$mg.sin(\alpha)=\mu (mg.cos(\alpha)-m\omega ^2 .r)$
Now I have:
$mg.x=\mu (mg.\sqrt{1-x^2}-m\omega^2 .r)$
But I don't know how to solve it, or how to solve it with your method

Yes, you can solve it that way too. Rearrange your equation to get the surd (the square root term) on one side and all else on the other. Can you see how to get rid of the surd then?

With regard to part C, my energy idea does not work. Try to get the differential equation that applies once slipping has started. (I believe it cannot be solved.)