CAF123
Gold Member
- 2,918
- 87
Homework Statement
Show that the ratio of atomic sphere to unit cell volume in HCP (hexagonal close packing) is 0.74.
Homework Equations
volumes of spheres, geometry
The Attempt at a Solution
I did the same problem for FCC and BCC and it was fine.
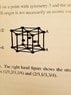
My unit cell structure is that shown below. I labeled the height between the two hexagonal planes by ##h## and the length of the equilateral triangles comprising the hexagon by ##2r##. If we then consider a 1/6 of this structure in the obvious way and orient it suitably so that one of the sides of the lower triangles coincides with the x-axis say, then the volume of 1/6 of this structure is $$V = 2 \int_0^{r} \int_0^{\sqrt{3}x} \int_0^h dx dy dz = \sqrt{3}hr^2.$$ Multiply this by 6 to get the whole volume of the unit cell structure shown below.
I would like to try to relate the height of this structure to the radius ##r## of the spheres so that in the ratio, I get cancellation. I am assuming that the three spheres on the middle layer of the structure (labeled B in the sketch) are wholly contained within the structure?