- #1
DaveC426913
Gold Member
- 22,479
- 6,142
Correct me if I'm wrong:
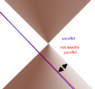
A parabola extends without limit toward parallel lines.
A hyperbola extends without limit toward diverging lines.
They have very different equations.
My question: is the former a specific instance of the latter?
Does a parabola = a hyperbola that happens to have parallel axes?
Some guy pointed me at this dumb video:
At 4:30 - 5:03 he says that is a parabola. It is not, since he literally shows the asymptotes at right angles.
A parabola extends without limit toward parallel lines.
A hyperbola extends without limit toward diverging lines.
They have very different equations.
My question: is the former a specific instance of the latter?
Does a parabola = a hyperbola that happens to have parallel axes?
Some guy pointed me at this dumb video:
At 4:30 - 5:03 he says that is a parabola. It is not, since he literally shows the asymptotes at right angles.
 In the video, they start off as vertical and horizontal axes, before he rotates them and turns them into asymptotes with some trickery.)
In the video, they start off as vertical and horizontal axes, before he rotates them and turns them into asymptotes with some trickery.)