Sefrez said:
Yes Gaussian surface. I know it would not be an ideal capacitor, I was trying to further enforce the idea that both must be equally charged rather than one simply being induced only. Here, I have drawn a diagram of what I was saying. However, maybe my idea of an induced charge is still not correct.
When the idea of capacitor was introduced in our studies, it was said that it consist of two parallel metal plates, one charged, the other grounded. The charges of one plate attract opposite charges in the grounded one, and repel like charges which go to the ground. It was also shown, that disconnected from the ground, this plate is really charged.
Instead of connecting to the ground, the capacitor plates can be connected to + and - terminals of a battery, and then both plates become charged with equal and opposite charges.
Now forget about capacitors, you have only a planar arrangement of charges. The electric field is E= q/(2εA)=σ/2ε, pointing away from the plane if q>0.
(σ is the surface charge density).
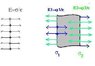
Take a metal plate, with the same charge q. You know that the charges move to the surface, and the electric filed is zero inside the metal. Allow unequal surface charge on the sides, but σ1+σ2=q/A
You can imagine two planes of charge instead of the metal. One produces the uniform electric field E1=σ1/(2ε), pointing away from the plane on both sides, the other plate produces E2=σ2/(2ε) .
The contributions of the planes add up and produce the resultant electric field. On the left of the metal sheet, it is E
left=-E1-E2=-(σ1+σ2)/(2ε). In the volume in the place of the metal, E
metal=E1-E2=(σ1-σ2)/(2ε)=0, and on the right E
right=(σ1+σ2)/(2ε).
The electric field is zero inside the metal, so there is equal surface charge on both sides: σ1=σ2=q/2.
At the end, the metal plate behaves like a single plane of charges, producing electric field of magnitude E=q/(2ε) on both sides.
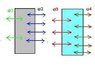
Place an other, uncharged metal plate parallel with the first one. Allow again surface charges, but the sum of them is zero in this case: σ3+σ4=0. Replace both metals with a pair of charged planes. Collect the contributions from each planes to the electric field.
On the left of the figure, E
left=-(σ1+σ2+σ3+σ4)/2ε.
Inside the grey volume, Eg=(σ1-σ2-σ3-σ4)/ε=0.
Between the metal sheets, E
middle=(σ1+σ2-σ3-σ4)/2ε
Inside the blue volume, Eb=(σ1+σ2+σ3-σ4)/2ε=0.
On the right, E
right=σ1+σ2+σ3+σ4)/2ε.σ3+σ4=0, so σ4=-σ3.
From the requirement of zero electric field inside the metals,
σ1-σ2=0, that is
σ1=σ2=q/(2A).
and
Eb=(σ1+σ2+σ3-σ4)/2ε=0=>q+2σ3=0=>σ3=-q/(2A),
σ4=-σ3=q/(2A).
Eleft=-(σ1+σ2+σ3+σ4)/2ε=-q/(2εA).
Eright=(σ1+σ2+σ3+σ4)/2ε=q/(2εA).
Emiddle=(σ1+σ2-σ3-σ4)/2ε=q/(2εA).
The new uncharged metal does not change the field of the charged one. The surface charge density is -q/2 next to the charged metal and opposite on the surface away from it.
You can apply this method when the second metal plate has some arbitrary charge.
ehild