- #1
Sefrez
- 126
- 0
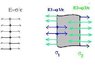
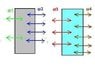
Why is it that the field magnitude between two plates in a parallel plate capacitor is given by q/(εA)? In my book it is stated that one plate is of charge +q and the other -q. But if each plate is charged, wouldn't you need to account for the electric field produced by both places making magnitude 2q/(εA)? That is, the sum of both field vectors.
My guess here is that only one plate is charged and the other one is given an induced charge. In other words, putting a Gaussian Field over the induced one results in zero flux. But I am unsure if this is correct?
My guess here is that only one plate is charged and the other one is given an induced charge. In other words, putting a Gaussian Field over the induced one results in zero flux. But I am unsure if this is correct?