sparkle123
- 172
- 0
Why can you do this?
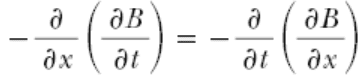
thanks!
thanks!
This discussion centers on the continuity of first and second partial derivatives of a function B, specifically in the context of magnetic fields. It is established that if B is defined as a function of variables x and t, and if its first and second partial derivatives are continuous, then certain mathematical operations can be performed. The conversation emphasizes that most naturally occurring phenomena, including magnetic fields, are infinitely differentiable, which supports the continuity of these derivatives.
PREREQUISITESStudents and professionals in mathematics, physics, and engineering who are looking to deepen their understanding of partial derivatives and their applications in real-world scenarios, especially in the context of magnetic fields.
sparkle123 said:Thanks!
How would you know if a function's first and 2nd partial derivatives are continuous?