Pendulum hitting a peg/conservation of energy

In summary, the conversation is about a pendulum with a light string and a small sphere swinging in a vertical plane. The string hits a peg located below the point of suspension. The task is to show that if the sphere is released from a height below the peg, it will return to the same height after the string strikes the peg. The equation used is Etotal = ΔK + ΔU = 0 for an isolated system. The attempt at a solution involves assuming that the only energy acting on the system is gravitational potential energy and solving for the unknown final height. Part b) of the task involves finding the minimum value of d when the pendulum is released from rest at the horizontal position and is to swing in a complete circle centered
  • #1
shawli
78
0

Homework Statement



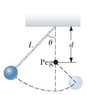
A pendulum comprising a light string of length L and a small sphere swings in the vertical plane. the string hits a peg located a distance d below the point of suspension. (Diagram attached below).

a) Show that if the sphere is released from a height below the peg, it will return to this height after the string strikes the peg.

b) Show that if the pendulum is released from rest at the horizontal position (θ = 90°) and is to swing in a complete circle centered on the peg, the minimum value of d must be 3L/5.

Homework Equations



Etotal = ΔK + ΔU = 0 for an isolated system

The Attempt at a Solution



I've attempted a) so far, but I'm not sure if it's right so I haven't yet tried b).

For a), I assumed that the only "energy" acting on the system in both the initial and final state would be gravitational potential energy. (No kinetic energy because it's released from rest, and v = 0 at the point where the pendulum turns to swing back).

So this gives me:

Ugf - Ugi = 0
mg(Lsinθ - d) - mgh = 0 (where 'h' is my unknown final height)
h = Lsinθ - d

I'm not sure if my "Lsinθ - d" value is correct for the initial height... would appreciate if someone could check this and/or lead me in the right direction if I'm wrong!
 

Attachments

  • p.png
    p.png
    5.3 KB · Views: 1,019
Last edited:
Physics news on Phys.org
  • #2
Also, I'm not really sure how to approach part b) at all...
 

1. What is a pendulum and how does it work?

A pendulum is a weight suspended from a fixed point that is able to swing freely back and forth due to the force of gravity. The motion of a pendulum is governed by the laws of physics, specifically the principles of conservation of energy and momentum.

2. How does a pendulum hitting a peg demonstrate the concept of conservation of energy?

When a pendulum is released, it begins to swing back and forth between two points. As it swings, it converts potential energy (due to its position at the top of its swing) into kinetic energy (due to its motion). When the pendulum hits a peg, it briefly stops and then continues to swing back and forth. This demonstrates the conservation of energy, as the energy is neither created nor destroyed, but rather transferred from one form to another.

3. What factors affect the energy of a pendulum hitting a peg?

The energy of a pendulum hitting a peg is affected by several factors, including the length of the pendulum, the mass of the weight, and the height at which the pendulum is released. These factors all influence the potential and kinetic energy of the pendulum, which in turn affect the force of impact on the peg.

4. How can we calculate the energy of a pendulum hitting a peg?

The energy of a pendulum hitting a peg can be calculated using the equation E = mgh, where E is energy, m is mass, g is the acceleration due to gravity, and h is the height at which the pendulum is released. By plugging in the appropriate values, we can determine the potential and kinetic energy of the pendulum at any point in its swing.

5. Why is the conservation of energy an important concept in physics?

The conservation of energy is a fundamental principle in physics that states that energy cannot be created or destroyed, but can only be transformed from one form to another. This concept is important because it allows us to predict and understand the behavior of physical systems, and it is a key component in many scientific theories and equations.

Similar threads

Foucault Pendulum at the North Pole
    • Introductory Physics Homework Help
Replies
9
Views
689
Pendulum swinging and hitting a peg
    • Introductory Physics Homework Help
Replies
1
Views
2K
Conservation of Energy of an Interrupted Pendulum
    • Introductory Physics Homework Help
Replies
1
Views
5K
Pendulum Conservation of Energy
    • Introductory Physics Homework Help
Replies
31
Views
2K
Calculating the Angle of a Pendulum Swing into a Peg
    • Introductory Physics Homework Help
Replies
3
Views
3K
What % of PEg must be converted in KE in order to double v?
    • Introductory Physics Homework Help
Replies
13
Views
2K
HW ?: Conservative Forces and Potential Energy
    • Introductory Physics Homework Help
Replies
2
Views
22K
How can the forces on a pendulum be calculated when encountering a peg?
    • Introductory Physics Homework Help
Replies
2
Views
10K
A pendulum with a ball and a string falls to wrap around another peg
    • Introductory Physics Homework Help
Replies
7
Views
10K
Can someone check my answer for this work-energy problem?
    • Introductory Physics Homework Help
Replies
5
Views
2K

Hot Threads

Recent Insights

Back
Top