Discussion Overview
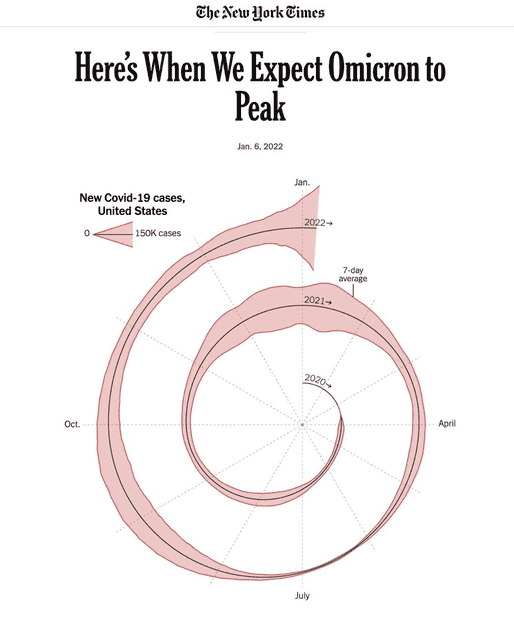
The discussion revolves around the interpretation of a periodic spiral graph presented in a New York Times article, focusing on its geometry, the non-uniform variation of radial distance, and the symmetry about the centerline. Participants explore the implications of these features in the context of data visualization.
Discussion Character
- Exploratory
- Debate/contested
- Technical explanation
Main Points Raised
- Some participants question the geometry of the graph, particularly why the radial distance varies non-uniformly, noting that the distance from the origin to November 2020 is much larger than from November 2020 to November 2021.
- There is a suggestion that the graph is spiral rather than merely polar, with the radial distance varying to accommodate bulging sections.
- Participants discuss the symmetry about the centerline, with some proposing it may be a design choice without significant meaning, while others challenge this view.
- One participant notes that the width of the path represents daily cases, while the angle indicates time in the year, suggesting the distance to the origin lacks significance.
- There are observations about potential non-symmetries in the graph, with some attributing these to a hand-drawn appearance and others questioning whether these are true asymmetries or optical illusions.
- Comparisons are made to an Archimedean spiral, with one participant suggesting that shifting the graph could yield a closer fit.
- Another participant expresses uncertainty about achieving a perfect fit for the graph's shape, indicating the complexity of the task.
Areas of Agreement / Disagreement
The discussion contains multiple competing views regarding the interpretation of the graph's features, particularly concerning symmetry and the significance of radial distance. No consensus is reached on these points.
Contextual Notes
Participants express uncertainty about the implications of the graph's design choices and the mathematical properties of the spiral. There are references to potential optical illusions and the challenges of accurately modeling the graph's shape.