Shreya
- 187
- 64
- Homework Statement
- I have always wondered what the phase of a wave means. I came up with something and I would really appreciate if someone could help me verify it and possibly find out flaws in it.
- Relevant Equations
- My textbook says: $$y = A \sin (kx - \omega t)$$ $$ y = A \sin k (x - vt)$$ $$y=A \sin (\frac {2\pi} {\lambda} (x - vt)$$ as ##\frac w k = v##
Let's begin my interpretation: (please refer the image below). There I have considered a point in the disturbance/wave (let's call it ##P##),(not a particle of the medium) and I follow it as the wave progresses. The solid curve is a Pic of the wave at ##t=0## and the dotted one is its Pic at some later time. The point in the disturbance has moved by ##vt##. So, the ##x - vt## in the equation can be interpreted as the intital distance of point P. On Dividing that by ##\lambda##, we get 'what part of the cycle was the point at initially' or the initial state. And on multiplying it by ##2\pi##, we are coverting that to 'what part of a complete revolution'. Finally taking the ##\sin## of it and multiplying with ##A## we get the ##y## value.
I would love to see comments on this & Understand any mistakes I've made. Thanks in Advance.
(Edit: Sorry for the blurry image, I have updated it)
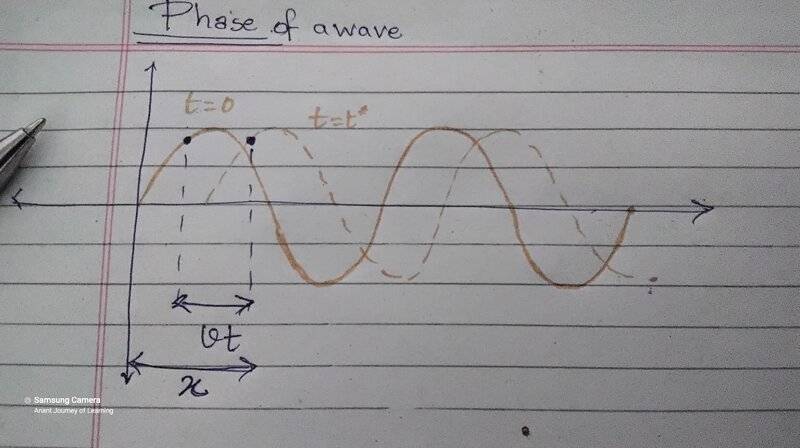
I would love to see comments on this & Understand any mistakes I've made. Thanks in Advance.
(Edit: Sorry for the blurry image, I have updated it)
Last edited: