nyxsilverjk
- 18
- 0
Homework Statement
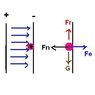
A 10 gram pith ball having a charge of 1μC is electrostatically attracted to one of the inside surfaces
of a large parallel plate capacitor by an electric field between the plates. The plates are vertically
oriented so that the electric field between the plates is horizontal. The distance between the plates of
the capacitor is 10 cm, and the coefficient of static friction between the pith ball and the plate is 0.5.
What is the minimum voltage needed to keep the ball from sliding down the plate from gravity? Draw
a picture to show all forces on the pith ball.
Homework Equations
I used F = μ(coef. of static)(mg) to find the amount of force it would take to overcome static friction then applied it to the equation V = (F/q charge)(d).
The Attempt at a Solution
I got 50 V as my answer but I don't know if this is right. It would be appreciated if someone could check behind me or tell me what I'm doing wrong.
Thanks.