Pivot Failure on Rotary Actuator

[Lesolee]

I have simplified the problem down to something like a physics textbook question, although this is a practical problem where the pivot on my rotary actuator has been damaged by a faulty driver which caused the armature to ram into the endstop.

Obviously this needs better protection. My problem is trying to relate the mechanics to the underlying physics.

Referring to the sketch, the mass M hits the endstop and decelerates pretty hard. The question is how to calculate the shear load on the pivot. Assume that the actuator is unpowered (not driven) when it hits the end stop and there are no other inertial loads than those shown.

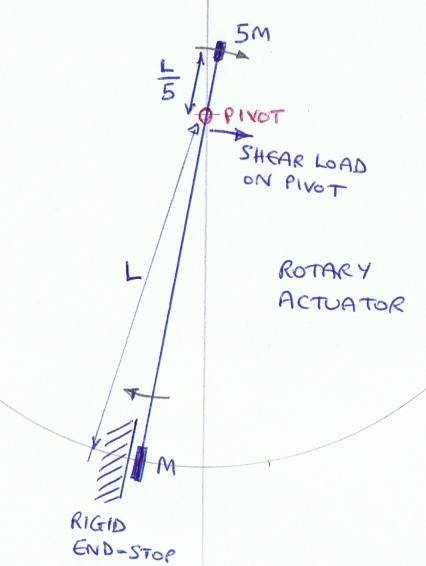
If the end-stop were perfectly rigid and the armature were perfectly rigid I can imagine the mass 5M continuing with its tangential velocity. But that doesn’t give a load force. I think it is reasonable to assume that the armature is rigid. Suppose the end-stop decelerates the whole actuator by 10g as a tangential deceleration on the mass M. How would that transfer to the pivot as a force? The pivot doesn’t have much “give” in it.

 

[Lesolee]

I guess that having reduced the problem to its essentials, the solution was closer to the surface. Another problem, the one with a bar and a force applied at one end, helped.

The deceleration of the mass M (and the rest of the armature) requires a force. The pivot has to exert an equal and opposite force or it will move. That’s it!

 

[Rx7man]

If you could put an end stop for the short end as well, that might reduce the load on the pivot significantly

 

[Tom.G]

How about considering "M" to be the pivot, the armature a lever, and the moving "5M" mass being the applied force at the end of a simple lever? Then compute the force at the point of the destroyed pivot.

 

[Lesolee]

If you could put an end stop for the short end as well, that might reduce the load on the pivot significantly

Yes, in principle the load on the pivot would be zero. Practically it would be difficult to tolerance the end-stops so they hit at exactly the same angle. The real problem is that the angle of the end stop is toleranced by a distance. This is much easier further from the pivot. The 5M mass is so close to the pivot that it could not realistically work.

 

[Lesolee]

How about considering "M" to be the pivot, the armature a lever, and the moving "5M" mass being the applied force at the end of a simple lever? Then compute the force at the point of the destroyed pivot.

Considering 'M' (in the earlier diagram, "C" in the diagram below) to be a pivot means an infinite force as it decelerates instantaneously. A moving "5M" mass does not give a force. Only a decelerating "5M" can give a force and since the deceleration is again instantaneous the force is infinite so this route doesn't help.

However, the more you abstract the problem, the more obvious the solution becomes. In order for the pivot to remain in place, F=R.

 

[Nidum]

(1) If the stop and the actuator assembly are very rigid compared to the lever arms then this problem can be analysed by considering the deflection of the lever arms during the crash event .

Not easy to get actual numbers from an analysis but it could be done if you have all the detailed dimensions of the components .

(2) A much easier way would be to calculate the breaking load for the shaft .

 

[Lesolee]

(1) If the stop and the actuator assembly are very rigid compared to the lever arms then this problem can be analysed by considering the deflection of the lever arms during the crash event .

The end-stops are actually pieces of foam, it is just pretty rigid foam. The lever arms are very rigid.

(2) A much easier way would be to calculate the breaking load for the shaft .

I plan on putting an accelerometer on the drive coil, C, and then using the known inertia to calculate the shear force.

 

[wrobel]

The question is how to calculate the shear load on the pivot. Ass

this is a simple problem. You need impact theory see for example Paul Appell Traité de mécanique rationnelle. I know nothing about English version of this book , in the Russian version the impact theory contains in the second volume

 

[Nidum]

The end-stops are actually pieces of foam, it is just pretty rigid foam. The lever arms are very rigid.

I plan on putting an accelerometer on the drive coil, C, and then using the known inertia to calculate the shear force.

But of a mystery then if you have a soft stop . Show me a picture or to scale drawing of the actual mechanism .

If the shaft broke then you can calculate what the breaking load was to a reasonable accuracy just from the shaft dimensions and material properties .

Fitting accelerometers would be an interesting thing to do but not essential to solve this problem

 

[Nidum]

Show me a picture of the broken shaft end as well . It is just possible that the shaft has failed in torsion rather than in simple shear .

 

[Lesolee]

If the shaft broke then you can calculate what the breaking load was to a reasonable accuracy just from the shaft dimensions and material properties .

Fitting accelerometers would be an interesting thing to do but not essential to solve this problem

Oh, I see what you mean now! No, the shaft didn't break, the "pivot" did. The pivot is not a simple bearing, it is a flexure. I didn't want to over-complicate the problem with unnecessary detail. The accelerometer is a way of quantifying the operating stress on the flexure, although to be fair it is going to be easier to do a locked rotor test to establish the maximum load when running normally.

There doesn't seem to be a "question answered" feature on this forum but I am happy that the correct answer has been found and would like to thank all respondents for helping me to reach the necessary level of simplicity to solve the problem.