FEAnalyst
- 348
- 149
- TL;DR
- How to calculate the stress and deflection for a cantilever plate using bending moment equation ?
Hi,
I'm trying to solve an exemplary case of a cantilever plate (one long edge fixed, all other edges free) subjected to pressure. I've already calculated this using approximation to beam of unit width and the results are good but I would like to use another method too. In a polish book I've found two examples - one plate with shorter edges simply supported and one with shorter edges clamped. I tried solving my example in a similar manner but the results are meaningless. The method is analogous to the approach used for beams - calculate stress from maximum bending moment and deflection from differential equation.
Here's a scheme of the plate:
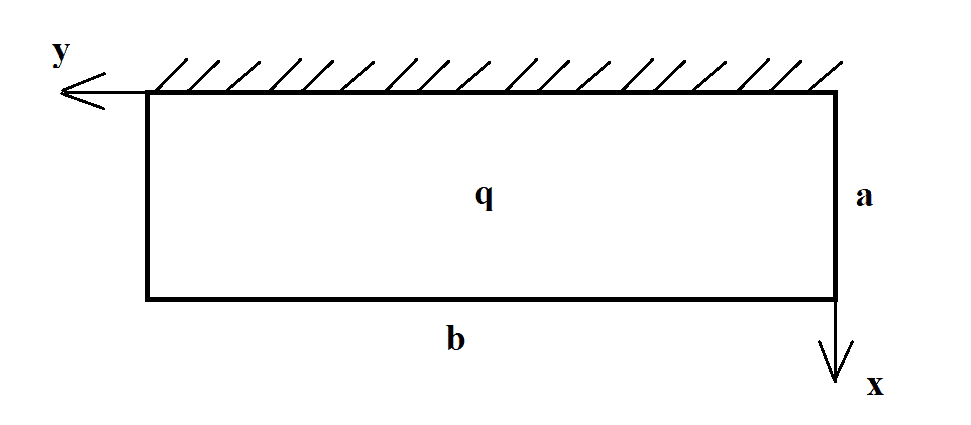
I was advised to use the following formula for bending moment: $$ \displaystyle{ M_{x}=\frac{qa^{2}}{2}-qax+ \frac{q x^{2}}{2}} $$ The bending moment equation for a plate is: $$\displaystyle{ D w^{\prime \prime}=-M_{x}}$$ Thus: $$\displaystyle{ D w^{\prime \prime}=- \frac{qa^{2}}{2}+qax- \frac{q x^{2}}{2}}$$ $$\displaystyle{ D w^{\prime}=- \frac{qa^{2}x}{2}+ \frac{q a x^{2}}{2} - \frac{q x^{3}}{6}+C_{1}}$$ $$\displaystyle{ D w=- \frac{qa^{2}x^{2}}{4}+ \frac{q a x^{3}}{6} - \frac{q x^{4}}{24}+C_{1}x+D_{1}}$$ Introducing boundary conditions to find constants of integration: $$\displaystyle{ x=0 \Longrightarrow w=0}$$ $$\displaystyle{ x=0 \Longrightarrow w^{\prime}=0}$$ $$\displaystyle{ C_{1}=\frac{qx \left( 3 a^{2} - 3ax + x^{2} \right) }{6}}$$ $$\displaystyle{ D_{1}=- \frac{q x^{2} \left( 6 a^{2} - 8ax + 3 x^{2} \right)}{24}}$$ $$\displaystyle{ Dw=- \frac{q a^{2} x^{2}}{4}+ \frac{q x^{2} \left( 3 a^{2} - 3ax + x^{2} \right)}{6}- \frac{qx^{2} \left( 6a^{2} - 8ax + 3x^{2} \right)}{24}+ \frac{qax^{3}}{6}- \frac{qx^{4}}{24}}$$ $$\displaystyle{ x=a \Longrightarrow w_{max}}$$ Now when I substitute ##a## to the previous equation I get ##Dw=0## which makes no sense.
When it comes to stresses, they will be highest at the fixed edge where ##x=0## so: $$M_{x \ max}=\frac{qa^{2}}{2}$$ $$\sigma_{x \ max}=\frac{M_{x \ max}}{\frac{h^{3}}{12}}$$ but when I substitute values, the stress results are completely incorrect.
What's wrong with these calculations ? Is the method itself not applicable in this case ? Examples from the book featured plates with symmetric boundary conditions but it wasn't mentioned that this approach won't work for asymmetric boundary conditions. Or maybe I just made some mistake ?
Thanks in advance for help
I'm trying to solve an exemplary case of a cantilever plate (one long edge fixed, all other edges free) subjected to pressure. I've already calculated this using approximation to beam of unit width and the results are good but I would like to use another method too. In a polish book I've found two examples - one plate with shorter edges simply supported and one with shorter edges clamped. I tried solving my example in a similar manner but the results are meaningless. The method is analogous to the approach used for beams - calculate stress from maximum bending moment and deflection from differential equation.
Here's a scheme of the plate:
I was advised to use the following formula for bending moment: $$ \displaystyle{ M_{x}=\frac{qa^{2}}{2}-qax+ \frac{q x^{2}}{2}} $$ The bending moment equation for a plate is: $$\displaystyle{ D w^{\prime \prime}=-M_{x}}$$ Thus: $$\displaystyle{ D w^{\prime \prime}=- \frac{qa^{2}}{2}+qax- \frac{q x^{2}}{2}}$$ $$\displaystyle{ D w^{\prime}=- \frac{qa^{2}x}{2}+ \frac{q a x^{2}}{2} - \frac{q x^{3}}{6}+C_{1}}$$ $$\displaystyle{ D w=- \frac{qa^{2}x^{2}}{4}+ \frac{q a x^{3}}{6} - \frac{q x^{4}}{24}+C_{1}x+D_{1}}$$ Introducing boundary conditions to find constants of integration: $$\displaystyle{ x=0 \Longrightarrow w=0}$$ $$\displaystyle{ x=0 \Longrightarrow w^{\prime}=0}$$ $$\displaystyle{ C_{1}=\frac{qx \left( 3 a^{2} - 3ax + x^{2} \right) }{6}}$$ $$\displaystyle{ D_{1}=- \frac{q x^{2} \left( 6 a^{2} - 8ax + 3 x^{2} \right)}{24}}$$ $$\displaystyle{ Dw=- \frac{q a^{2} x^{2}}{4}+ \frac{q x^{2} \left( 3 a^{2} - 3ax + x^{2} \right)}{6}- \frac{qx^{2} \left( 6a^{2} - 8ax + 3x^{2} \right)}{24}+ \frac{qax^{3}}{6}- \frac{qx^{4}}{24}}$$ $$\displaystyle{ x=a \Longrightarrow w_{max}}$$ Now when I substitute ##a## to the previous equation I get ##Dw=0## which makes no sense.
When it comes to stresses, they will be highest at the fixed edge where ##x=0## so: $$M_{x \ max}=\frac{qa^{2}}{2}$$ $$\sigma_{x \ max}=\frac{M_{x \ max}}{\frac{h^{3}}{12}}$$ but when I substitute values, the stress results are completely incorrect.
What's wrong with these calculations ? Is the method itself not applicable in this case ? Examples from the book featured plates with symmetric boundary conditions but it wasn't mentioned that this approach won't work for asymmetric boundary conditions. Or maybe I just made some mistake ?
Thanks in advance for help