Please explain this doubt about a block sliding question

[Benjamin_harsh]

Homework Statement

A block of mass M is released from point P on a rough inclined
plane with inclination angle θ, shown in the figure below. The coeffucient
of friction is μ. if μ < tan θ, then time taken by the block to reach another
point Q on the inclined plane, where PQ = s, is

Relevant Equations

What is the meaning of " PQ = s" in the question?

How $t = \large\sqrt\frac{2s}{a}$?

Sol:

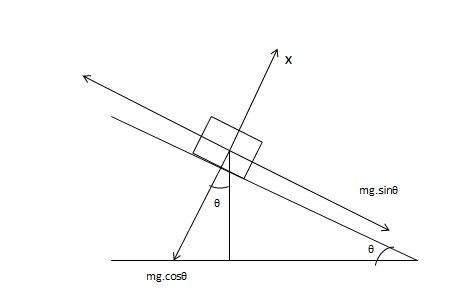
$Mg.sinθ - μMg.cosθ = ma$
$a = g.sinθ - μg.cosθ$

Now $S = ut + \large\frac{1}{2}\normalsize at^{2}$

but $u = 0$

$t = \large\sqrt\frac{2s}{a} = \sqrt\frac {2s}{gcosθ(tanθ- μ)}$

My questions:

What is the meaning of " PQ = s" in the question?

How $t = \large\sqrt\frac{2s}{a}$?

How $a =gcosθ(tanθ- μ)$ in that last square root step?

 

[Replusz]

s=a/2 t^2 is a standard formula, that's how he got a=sqrt (...)

a=g(sin theta - mu * cos theta) just comes from considering forces parallel and perpendicular to the plane where it slides. PQ=s just means that instead of always writing "PQ" he will write "s" because its shorter.

 

[Benjamin_harsh]

Explain this equation $Mg.sinθ - μMg.cosθ = ma$ ? I know standard sliding block equation: $w·sinθ – μkN = 0$ &

$N – w·cosθ = 0$How to understand $μ < tan θ$?

 

[Replusz]

Explain this equation $Mg.sinθ - μMg.cosθ = ma$ ? I know standard sliding block equation: $w·sinθ – μkN = 0$ &

$N – w·cosθ = 0$How to understand $μ < tan θ$?

Yes you just take N=W cos theta and put it into te standard sliding block equation. Then you immediately get what you want

mu<tan(theta) because otherwise the block won't start sliding, the friction holds it in place. You can see that the equation of t=sqrt (...) gives you a complex number

 

[kuruman]

I know standard sliding block equation: w⋅sinθ–μkN=0w·sinθ – μkN = 0

This equation is not standard for a block sliding down an incline with only gravity and incline forces acting on it. It is correct only if the acceleration of the block along the incline is zero.

 

[Replusz]

Lol you right mate. There is so much wrong with how he labels stuff i didnt even realize the =0 at the end

Yes, so its not 0. Its acceleration

 

[Benjamin_harsh]

No need of $ΣF_{X} = 0$ & $ΣF_{y} = 0$ for this sliding block problem? If yes, when to use $ΣF_{X} = 0$ & $ΣF_{y} = 0$ ?

 

[Replusz]

Jesus.

N=Mk, where k is my acceleration, M is mass, and N is force. So now if we k=0 then sum(N)=0 but ONLY when k =0! But then it work good!

In this problem k not is 0 because you the acceleration have in parralel with the" slide ".

 

[kuruman]

No need of $ΣF_{X} = 0$ & $ΣF_{y} = 0$ for this sliding block problem? If yes, when to use $ΣF_{X} = 0$ & $ΣF_{y} = 0$ ?

The general form for the two equations that is always correct to write down is
$ΣF_{x} = ma_x~;~ ~ΣF_{y} = ma_y$ where $a_x$ and $a_y$ are the components of the acceleration. The sum of the forces in either direction is zero only if you have good reason to believe that it is. In this particular problem you have a block sliding down the incline along the $y$-axis. This is enough reason to know something about the acceleration in the $x$-direction. What is that? You are also told that the coefficient of (static) friction is less than $\tan\theta.$ That says something about the acceleration in the $y$-direction. What could that be? Hint: What is the statement of the problem trying to tell you with $\mu<\tan\theta$?

 

[Benjamin_harsh]

The sum of the forces in either direction is zero only if you have good reason to believe that it is.

how can I tell The sum of the forces in either direction is zero ? Good reasons like what?

 

[kuruman]

The net force in either direction is zero if the acceleration in that direction is zero. Of the two directions, perpendicular and parallel to the incline, is there a direction along which you can tell for sure that the acceleration is zero and hence the net force is also zero? Hint: Acceleration is a measure of change in velocity.

 

[Benjamin_harsh]

Acceleration if no friction exist; $a_{x} = mg.sinθ$

Acceleration if friction exist; $a = g.sinθ - µ_{k}.g.cosθ$ (I am not sure whether it is $μ_{s}$ or $µ_{k}$ in this equation)

Are these equations correct for sliding block equations?

 

[kuruman]

Acceleration if no friction exist; $a_{x} = mg.sinθ$
[\quote]
Incorrect. There should be $m$ on the right side.

Acceleration if friction exist; $a = g.sinθ - µ_{k}.g.cosθ$ (I am not sure whether it is $μ_{s}$ or $µ_{k}$ in this equation)

This is correct but only if the gravity and the incline exert forces on the block. You should use $\mu_k$ if the block is moving relative to the surface. You may use $\mu_s$ in that equation if the block is at rest relative to the surface but only if the block is just on the verge to start sliding.

Are these equations correct for sliding block equations?

They are correct but subject to the conditions stated above for the direction parallel to the surface. What about the direction perpendicular to the surface? What can you say about that?