nyrychvantel
- 14
- 0
1. A curve passes through the point (\pi/2 , 0) and it's gradient at any point (x,y) on the curve is (sin x)(1 - sin x), find the equation of the normal to the curve at the point x = \pi.
I tried to sub x = \pi, then dy/dx = 0
so that means gradient of the tangent at x = \pi is 0
So, can I say the gradient of the normal is also = 0?
However it contradicts me as I know (Grad. of tgt.)(Grad. of normal) = -1
0 * 0 \neq -1
How can I show the equation of the normal to my examiners with mathematical explanations?
2.
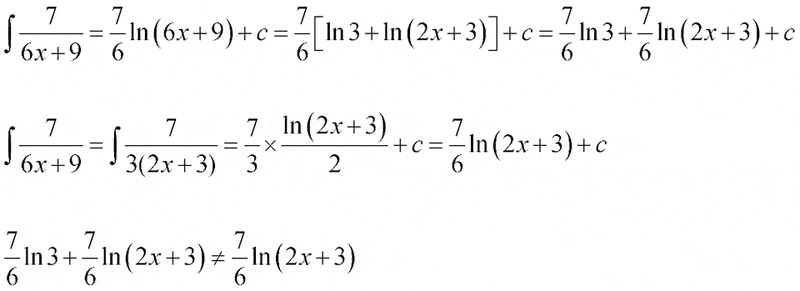
Can someone please explain to me why there are two different results(if i ignore the c)? Or did I do the question wrongly?
3. \int\frac{3-x}{1-x}
How can I solve this question? I'm totally stucked because there is a x in the numerator. So is the "ln" method still applicable here?
Thanks!
I tried to sub x = \pi, then dy/dx = 0
so that means gradient of the tangent at x = \pi is 0
So, can I say the gradient of the normal is also = 0?
However it contradicts me as I know (Grad. of tgt.)(Grad. of normal) = -1
0 * 0 \neq -1
How can I show the equation of the normal to my examiners with mathematical explanations?
2.
Can someone please explain to me why there are two different results(if i ignore the c)? Or did I do the question wrongly?
3. \int\frac{3-x}{1-x}
How can I solve this question? I'm totally stucked because there is a x in the numerator. So is the "ln" method still applicable here?
Thanks!