- #1
chwala
Gold Member
- 2,650
- 351
- Homework Statement
- see attached question and ms
- Relevant Equations
- integration
Find question here;
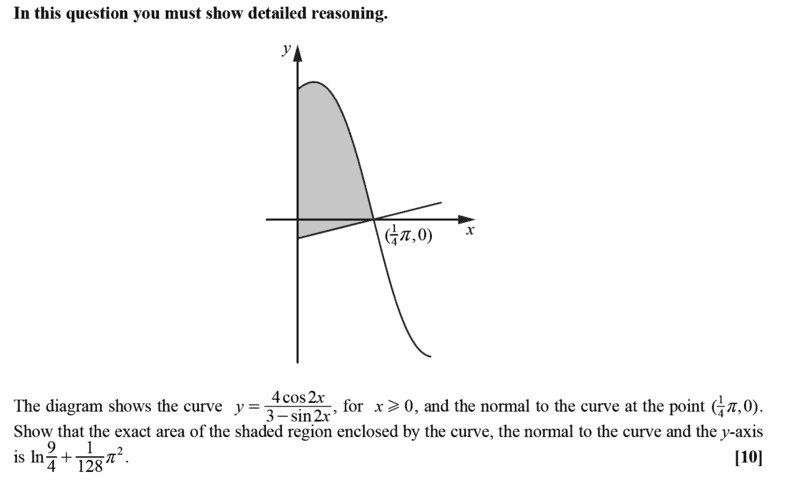
Find solution here;

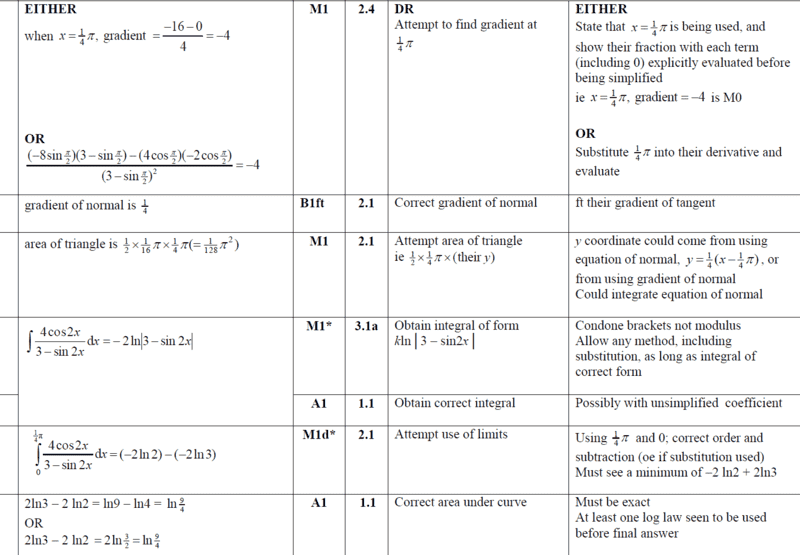
I used the same approach as ms- The key points to me were;
* making use of change of variables...
$$A_{1}=\int_0^\frac{π}{4} {\frac {4\cos 2x}{3-\sin 2x}} dx=-2\int_3^{-2} {\frac {du}{u}}= 2\int_2^3 {\frac {du}{u}}=2\ln 3-2\ln2=\ln 9 - \ln 4=\ln \frac{9}{4}$$
Now to find the other area subtended by the normal, x- axis and y- axis;
We make use of quotient rule. $$y'=\frac{(3-\sin 2x)(-8\sin 2x)-(4\cos 2x)(-2\cos 2x)}{(3-\sin 2x)^2}$$
the x-value =##\frac{π}{4}## can be substituted here directly and this is what i wanted to share. The gradient of the curve at the point where ##x=\frac{π}{4}## will be
$$y'=\frac{(3-1)(-8)-(0)(0)}{(3-1)^2}=\frac{2⋅-8}{2^2}=-4$$
Now for the given straight line equation, which is a Normal to the curve; We know that,
##y=mx +c##. It follows that,
##0=\frac{1}{4}⋅\frac{π}{4}+c##
##⇒ c=-\frac{π}{16}##
$$A_{2}=\frac {1}{2}⋅\frac{1}{4}⋅ \frac{π}{16}=\frac{π^2}{128}$$
$$A_{Required}= A_{1}+A_{2}=\ln \frac{9}{4}+ \frac{π^2}{128}$$
Find solution here;
I used the same approach as ms- The key points to me were;
* making use of change of variables...
$$A_{1}=\int_0^\frac{π}{4} {\frac {4\cos 2x}{3-\sin 2x}} dx=-2\int_3^{-2} {\frac {du}{u}}= 2\int_2^3 {\frac {du}{u}}=2\ln 3-2\ln2=\ln 9 - \ln 4=\ln \frac{9}{4}$$
Now to find the other area subtended by the normal, x- axis and y- axis;
We make use of quotient rule. $$y'=\frac{(3-\sin 2x)(-8\sin 2x)-(4\cos 2x)(-2\cos 2x)}{(3-\sin 2x)^2}$$
the x-value =##\frac{π}{4}## can be substituted here directly and this is what i wanted to share. The gradient of the curve at the point where ##x=\frac{π}{4}## will be
$$y'=\frac{(3-1)(-8)-(0)(0)}{(3-1)^2}=\frac{2⋅-8}{2^2}=-4$$
Now for the given straight line equation, which is a Normal to the curve; We know that,
##y=mx +c##. It follows that,
##0=\frac{1}{4}⋅\frac{π}{4}+c##
##⇒ c=-\frac{π}{16}##
$$A_{2}=\frac {1}{2}⋅\frac{1}{4}⋅ \frac{π}{16}=\frac{π^2}{128}$$
$$A_{Required}= A_{1}+A_{2}=\ln \frac{9}{4}+ \frac{π^2}{128}$$
Last edited: