SUMMARY
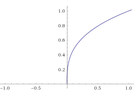
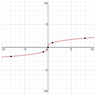
The discussion centers on the discrepancies observed when plotting the function \(y=x^{\frac{1}{3}}\) using different plotters. The first plotter appears to misinterpret the calculation for negative values of \(x\), likely due to an improper application of logarithmic functions, which do not support negative inputs. The power identity \(a^{b\cdot c}=(a^b)^c\) fails for negative bases when fractional powers are involved, leading to incorrect results. It is established that \(x^{1/3}\) is generally undefined for negative \(x\) unless specifically defined as \(-(-x)^{1/3}\).
PREREQUISITES
- Understanding of fractional powers and their properties
- Familiarity with logarithmic functions and their limitations
- Knowledge of graphing tools and their algorithms
- Basic principles of complex numbers and their relation to negative bases
NEXT STEPS
- Research the behavior of fractional powers in mathematical software
- Learn about the limitations of calculators when handling negative bases
- Explore the definition and properties of complex numbers in relation to roots
- Investigate alternative graphing tools that handle negative inputs correctly
USEFUL FOR
Mathematicians, educators, students in calculus, and anyone involved in graphing functions or analyzing mathematical software outputs.