Point in a rectangle given angles only

[Hepth]

Homework Statement

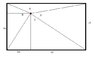
Imagine you're given a rectangle, with lengths LX and LY.

Now we place a point somewhere inside this rectangle, we don't know where it is.
What we DO know, is the angle between lines from the corners to that point. (such that if it was at the center, and the point a square, every angle would be 90, or pi/2)

Is there a way to calculate, from given angles, the x and y position of this point.

The Attempt at a Solution

I tried by hand and mathematica. I can't seem to do it, neither can mathematica. Has anyone seen or tried this before?

Ill draw it up just in case you don't understand the question.

Find the coordinates ->ABCD are the full angles from semi-diagonal to semi-diagonal. The straight lines are just for seeing xo and yo.

 

[LCKurtz]

You are aware that even if/when you solve it, there will generally be four locations by symmetry, right?

 

[Hepth]

Yes, but that isn't an issue. I can resolve that because, like I said this isn't really a problem, and I SORT of know which lengths of diagonals are larger than the others, but not their size. From which info I can sort it out.

Has anyone tried this? I feel like, since there are three independent angles that should give us MORE than enough information about the point, but I think it ends up being a solution to some transcendental equations.

 

[LCKurtz]

I think sometimes 2 of the angles is enough. I programmed it up in Maple. It choked trying to find an explicit solution. When I put in specific numbers it sometimes gave me a numeric solution that looked right when I plotted it, but sometimes it gave me a clearly wrong "solution". Not much help I'm afraid. If you have a specific set of numbers I could try them. Otherwise, it doesn't look good.

 

[Hepth]

I figured it out. Basically you need to do it by had with the tangents and recognize that Tan[ArcTan[x]+ArcTan[y]]== (x+y)/(1-xy)

Reminds me of special relativity... hehe :)

But with that you can avoid all of the matlab/mathematica's internal problems, throw in a bunch of absolute values, and get a solution, though its really ugly.

I ended up going a different route though, using two other angles, because it would be less calculations per second.