brotherbobby
- 807
- 178
- Homework Statement
- Indicate the points on the place ##xOy## which satisfy the equation : ##\mathbf{y+|y|-x-|x| = 0}##.
- Relevant Equations
- The modulus of a variable ##|x| = x\; \text{if}\; x\geq 0## and ##-x\; \text{if}\; x\leq 0##
We can write the equation given as ##y+|y| = x+|x|##
This has a few conditions.
(1) If ##\underline{y\geq 0\; \text{and}\; x\geq 0}##, we obtain ##2y = 2x \Rightarrow \boxed{y = x}##.
(2) If ##\underline{y\geq 0\; \text{and}\; x < 0}##, we obtain ##2y = 0 \Rightarrow \boxed{y = 0}##.
(3) If ##\underline{y < 0\; \text{and}\; x\geq 0}##, we obtain ##2x = 0\Rightarrow \boxed{x = 0}##
(4) If ##\underline{y < 0\; \text{and}\; x < 0}##, we obtain the trivial solution ##0 = 0##. But since 0 =0 always, this means all values of ##y<0\;\text{and}\; x<0## are solutions to the equation.
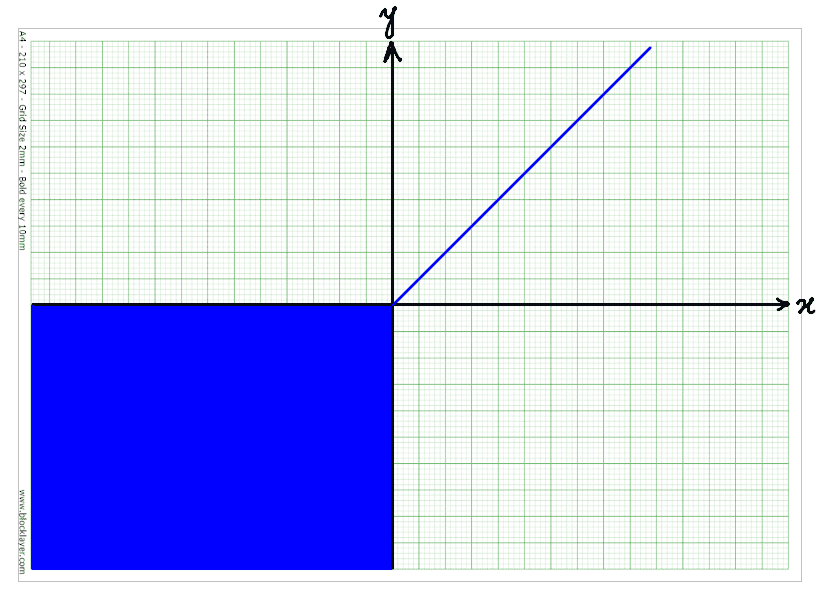I plot the graph alongside for the solution and regions.
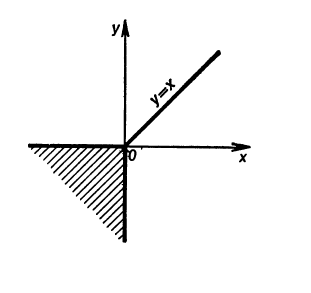
On the left is the solution from the book.
Though my answer looks correct, is the reasoning alright?
This has a few conditions.
(1) If ##\underline{y\geq 0\; \text{and}\; x\geq 0}##, we obtain ##2y = 2x \Rightarrow \boxed{y = x}##.
(2) If ##\underline{y\geq 0\; \text{and}\; x < 0}##, we obtain ##2y = 0 \Rightarrow \boxed{y = 0}##.
(3) If ##\underline{y < 0\; \text{and}\; x\geq 0}##, we obtain ##2x = 0\Rightarrow \boxed{x = 0}##
(4) If ##\underline{y < 0\; \text{and}\; x < 0}##, we obtain the trivial solution ##0 = 0##. But since 0 =0 always, this means all values of ##y<0\;\text{and}\; x<0## are solutions to the equation.
On the left is the solution from the book.
Though my answer looks correct, is the reasoning alright?