Math Amateur
Gold Member
MHB
- 3,920
- 48
I am reading D. J. H. Garling's book: "A Course in Mathematical Analysis: Volume II: Metric and Topological Spaces, Functions of a Vector Variable" ... ...
I am focused on Chapter 11: Metric Spaces and Normed Spaces ... ...
I need some help with the polarization formula for the complex case ...
Garling's statement of the polarization formulae reads as follows:

In the above text from Garling we read the following:" ... ... in the complex case we have the polarization formula## \langle x,y \rangle = \frac{1}{4} \left( \sum_{ j = 0 }^3 i^j \| x + i^j y \|^2 \right) ## ... ... "
Can someone please demonstrate how to prove that ##\langle x,y \rangle = \frac{1}{4} \left( \sum_{ j = 0 }^3 i^j \| x + i^j y \|^2 \right)## ...?Help will be appreciated ...
Peter
==========================================================================================***NOTE***
It may help readers of the above post to know Garling's notation and approach to inner-product spaces ... ... so I am providing the same ... as follows:




Hope that helps ...
Peter
I am focused on Chapter 11: Metric Spaces and Normed Spaces ... ...
I need some help with the polarization formula for the complex case ...
Garling's statement of the polarization formulae reads as follows:
In the above text from Garling we read the following:" ... ... in the complex case we have the polarization formula## \langle x,y \rangle = \frac{1}{4} \left( \sum_{ j = 0 }^3 i^j \| x + i^j y \|^2 \right) ## ... ... "
Can someone please demonstrate how to prove that ##\langle x,y \rangle = \frac{1}{4} \left( \sum_{ j = 0 }^3 i^j \| x + i^j y \|^2 \right)## ...?Help will be appreciated ...
Peter
==========================================================================================***NOTE***
It may help readers of the above post to know Garling's notation and approach to inner-product spaces ... ... so I am providing the same ... as follows:
Hope that helps ...
Peter
Attachments
-
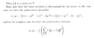 Garling - Polarization Formulae for Inner Product Spaces ,,, ,,,.png15.5 KB · Views: 1,461
Garling - Polarization Formulae for Inner Product Spaces ,,, ,,,.png15.5 KB · Views: 1,461 -
 Garling - 1 - Start of Section on Inner-Product Spaces ... PART 1 ... .png29.1 KB · Views: 741
Garling - 1 - Start of Section on Inner-Product Spaces ... PART 1 ... .png29.1 KB · Views: 741 -
 Garling - 2 - Start of Section on Inner-Product Spaces ... PART 2 ... .png25.3 KB · Views: 688
Garling - 2 - Start of Section on Inner-Product Spaces ... PART 2 ... .png25.3 KB · Views: 688 -
 Garling - 3 - Start of Section on Inner-Product Spaces ... PART 3 ... .png23.3 KB · Views: 654
Garling - 3 - Start of Section on Inner-Product Spaces ... PART 3 ... .png23.3 KB · Views: 654 -
 Garling - 4 - Start of Section on Inner-Product Spaces ... PART 4 ... .png23.8 KB · Views: 1,013
Garling - 4 - Start of Section on Inner-Product Spaces ... PART 4 ... .png23.8 KB · Views: 1,013