zak100
- 462
- 11
Homework Statement
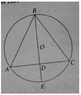
In the figure Q image2.jpeg (attached), equilateral triangle ABC is inscribed in circle O, whose radius is 4. Altitude BD is extended until it intersects the circle at E. What is the length of DE?
Solution figure is attached. They formed a right angled triangle & calling it 30-60-90. I know the 90 degree angle but how to find the vertices with 30 degrees & 60 degrees angle?
Homework Equations
Pythagorous thorem:
sqr(a) + sqr(b) = sqr(c)
Sides of a 30-60-90 tirangle are : x, x * sqrt(3), 2 * x (hypotenuse)
The Attempt at a Solution
The solution image is attached. They connected A with O. It then forms a triangle AOD. AO is 4 because its radius (no problem). Therefore 2 * x = 4, so x = 2, so length of smaller side is 2. But which side is smaller. For this we must know the angles associated with the vertices A & O.
Some body please tell me the angle formed by the vertices A & O, how should we find this?
Zulfi.
Zulfi.