Potential energy as a function of the square of this angle

[Tony Hau]

Homework Statement

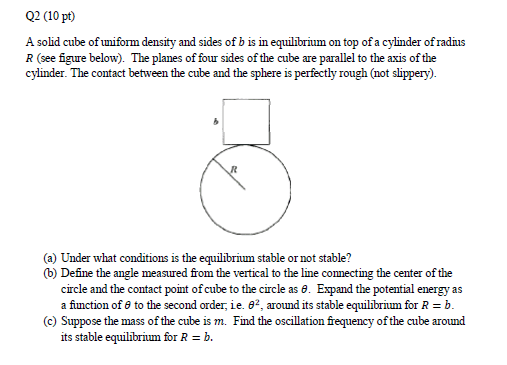
Define the angle measured from the vertical to the line connecting the center of the
circle and the contact point of cube to the circle as 𝜃. Expand the potential energy as
a function of 𝜃 to the second order; i.e. 𝜃^2, around its stable equilibrium for 𝑅 = 𝑏.

Relevant Equations

U(𝜃) = mgh(𝜃) = mg[(R+b/2)cos𝜃 +R𝜃sin𝜃]

The problem of my question is the b part below:

I know that the potential energy is just the gravitational potential energy, which is mgh(𝜃) = mg[(R+b/2)cos𝜃 +R𝜃sin𝜃], derived from the geometry. The equilibrium point is at 𝜃=0 and the system is a stable equilibrium for R>b/2. However, I have no idea how I can convert the potential energy as a function of the square of 𝜃, as stated by the question.

 

[mitochan]

Do Taylor expansion of
$$\cos\theta$$ and $$\theta \sin \theta$$
in $U(\theta)$ up to $\theta^2$.

 

[Tony Hau]

Do Taylor expansion of
$$\cos\theta$$ and $$\theta \sin \theta$$
in $U(\theta)$ up to $\theta^2$.

Thanks. It sounds reasonable! Here is the answer of the question. I am thinking why this method also works. Basically I don't quite get the logic behind. I know that the first order derivative of U is force. But I don't understand what 1/2 of the second order derivative represents.

 

[Tony Hau]

Here is my solution for the two methods. They are inconsistent.

 

[mitochan]

The both coincide in the exact calculation. Please try again.