rasalzari
- 27
- 2
<Mentor's note: moved from a general forum and therefore no template>
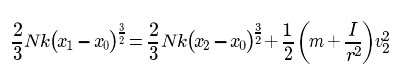
This is the equation of potential energy in rubber bands, however, I don't know how to calculate the inertia of the arm of catapults or get the k constant. And what does n mean? Basically, i don't understand the whole equation.
The energy balance, where N is the number of rubber bands, k is the spring constant of a single rubber band, x0 is the unstretched length of a rubber band, m the mass of the ball, and I is the moment of inertia of the arm.
Can someone please show me an example of how to calculate this?
I used a marshmallow which is 0.007 kg, I stretched the catapults to 0.1 m, it has an angle of 35 degrees
range=0.793
initial velocity=2.88 m/s
time=0.337 s
max height=0.139 m
horizontal velocity=2.36 m/s
vertical velocity=1.65 m/s
Thats all i know and i hope it helps! please help me figure this out!
This is the equation of potential energy in rubber bands, however, I don't know how to calculate the inertia of the arm of catapults or get the k constant. And what does n mean? Basically, i don't understand the whole equation.
The energy balance, where N is the number of rubber bands, k is the spring constant of a single rubber band, x0 is the unstretched length of a rubber band, m the mass of the ball, and I is the moment of inertia of the arm.
Can someone please show me an example of how to calculate this?
I used a marshmallow which is 0.007 kg, I stretched the catapults to 0.1 m, it has an angle of 35 degrees
range=0.793
initial velocity=2.88 m/s
time=0.337 s
max height=0.139 m
horizontal velocity=2.36 m/s
vertical velocity=1.65 m/s
Thats all i know and i hope it helps! please help me figure this out!

