workhorse123
- 1
- 0
- Homework Statement
- The charge density in the region
-z’<z<z’
depends only on z; that is,
p=p’cos(pi z/z’)
where p’ and z’ are constants. Determine the potential in all regions of space
- Relevant Equations
- Poisons equation, laplace equation
for the boundary conditions for this problem I understand that Electric field and Electric potential will be continuous on the boundaries.
I also know that I can set the reference point for Electric potential, wherever it is convenient. This gives me the fifth boundary condition. I am confused at where I find the last boundary condition.
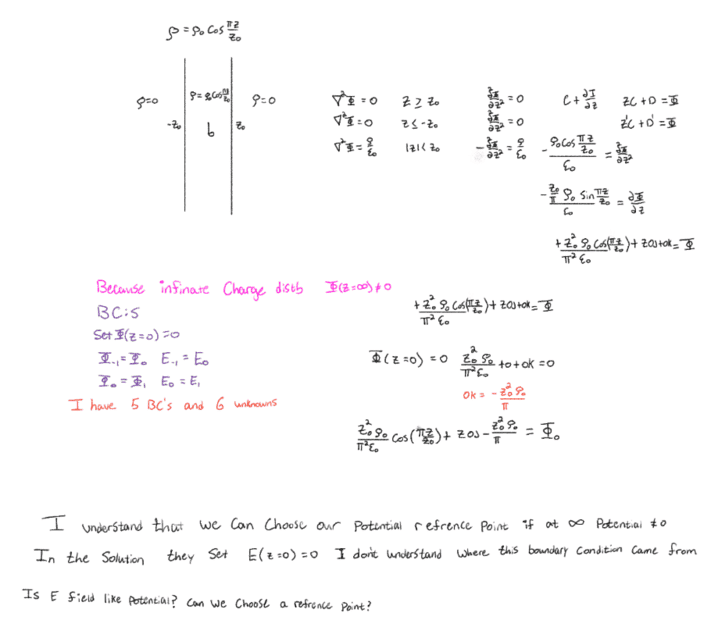
I also know that I can set the reference point for Electric potential, wherever it is convenient. This gives me the fifth boundary condition. I am confused at where I find the last boundary condition.
Attachments
Last edited by a moderator: