EM: Separation of variables to find magnetic induction

[phys194]

Homework Statement

Find the magnetic induction in the magneto-optic fluid

Relevant Equations

B = -grad(psi), grad^2 psi = 0

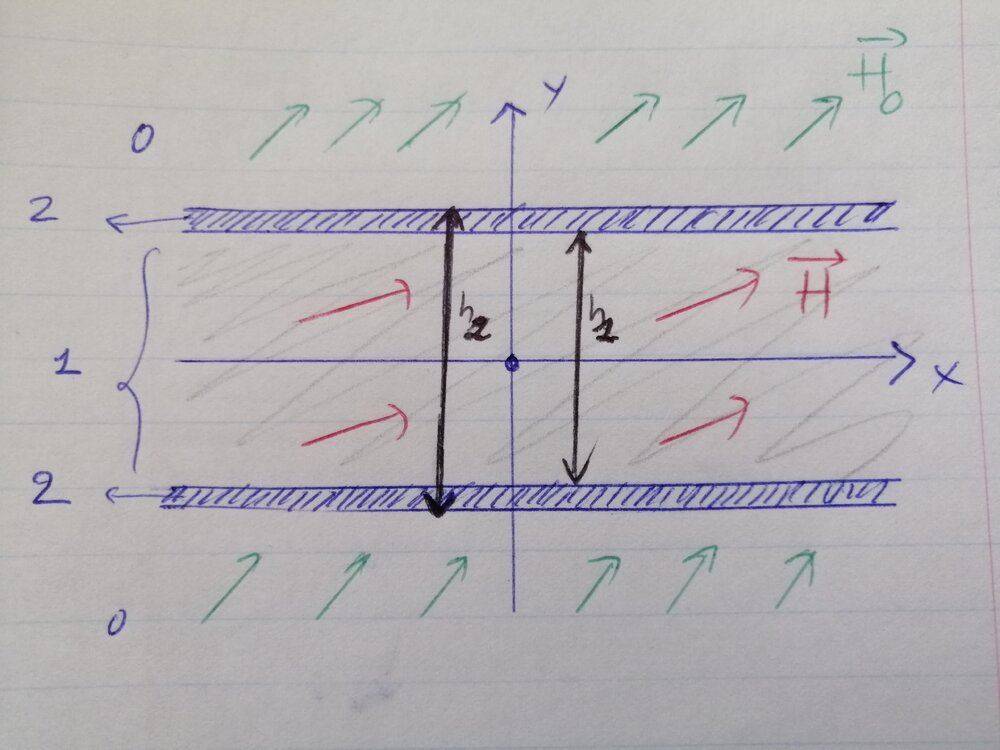
Consider the static field configuration shown in the image. There are three layers: 0 = vacuum, 1 = magneto-optic fluid and 2 = covering shell. Each of these layers have their own permittivity and permeability (ε_i,μ_i) (isotrope). A uniform electric field H_0 = H_0/sqrt(2) * (e_x + e_y) is applied in vacuum (layer 0) using an electromagnet. This results in a static field H in the magneto-optic fluid core (layer 1). I need to find the magnetic induction in the magneto-optic fluid, assuming that the fluid container is infinite in the x- and z-direction.

My attempt was as follows:

As J = 0 (free current density) everywhere and each of the layers (or rather, regions) are simply connected, we can work with a scalar magnetic potential ψ and B = - grad (ψ). As the problem is z-independent, I would go for separation of variables (in Cartesian coordinates). So, ψ(r) = X(x)Y(y) and from Gauss' magnetic law follows that the magnetic potential needs to satisfy the Laplace equation. Therefore, X"Y + XY"=0, resulting in solutions of the form X(x)=Asin(kx)+Bcos(kx) and Y(y) = Ce^(-ky)+De^(ky) for some constant k (or the other way around, i.e. X = e^... and Y=sin+cos?). Now, we know the general solution for ψ, and to have the particular solution for this problem, we need to apply boundary conditions that ψ has to satisfy.

I'm having trouble finding which boundary conditions need to be satisfied by ψ. No initial values of this potential have been given. I would assume that we need to look at the boundaries between each layer and since the normal component of the magnetic induction continuous. The main problem for me here is that I'm not sure if layer 2 does actually have a magnetic field (resulting from H_0), as this is not drawn on the image?

Moreover, I'm not sure what to do with the limiting cases: as y and x approach infinity, does the potential have to disappear? For Y(y) this would mean that Y(y)=constant, because the magnetic field (and thus induction, because of the isotropy of the problem) is uniform and constant for y = infinity and y = - infinity.

Thank you for taking the time to help me out.

 

[phys194]

Updates: after a better analysis of the symmetry of the problem (transformations x-> -x, y-> -y leave everything intact), I was able to find that X(x)=Acos(kx)+Bsin(kx) and Y(y) = Ce^(ky)+De^(-ky) OR Ecosh(ky)+Fsinh(ky). The symmetry of the problem implies that no odd terms can appear in the expression that will be derived, so B=F=0 and moreover C=D. For y>h2/2 we can select Y=Ce^(-ky), but because Y is even, we need to have that k=0 (otherwise evenness is not satisfied). We recompute the solution of the -now- homogeneous Laplace equation. Conclusion: in the vacuum region X=Ax+B and Y=Cy+D. Then using the given field H_0, we can determine that the potential in vacuum is given by -μ_0*H_0/√2 (x+y), which does indeed give H_0 when considering the gradient. So now, how can I use this to find H_1?

 

[Delta2]

This seems like an interesting problem cause you are looking for a scalar potential $\psi$ for the magnetic field such that $\vec{B}=-\nabla\psi$ and by applying gauss's law $\nabla\cdot\vec{B}=0$ for the magnetic field to end up with Laplace equation $\nabla^2\psi=0$. All of this assuming that the rotational part of $\vec{B}$ is zero because $\nabla\times\vec{B}=\mu_0\vec{J}=0$ if we ignore the $\frac{d\vec{E}}{dt}$ term that appears at the Maxwell-Ampere equation (assuming that the E-field from the electromagnet is low frequency? not sure I understand that part correctly). I also I am not familiar with the concept of opto-magnetic fluid.

Anyway I don't feel confident on working on this problem, I ll request for help from @Charles Link or @TSny that are both experts in classical EM.

 

[phys194]

This seems like an interesting problem cause you are looking for a scalar potential $\psi$ for the magnetic field such that $\vec{B}=-\nabla\psi$ and by applying gauss's law $\nabla\cdot\vec{B}=0$ for the magnetic field to end up with Laplace equation $\nabla^2\psi=0$. All of this assuming that the rotational part of $\vec{B}$ is zero because $\nabla\times\vec{B}=\mu_0\vec{J}=0$ if we ignore the $\frac{d\vec{E}}{dt}$ term that appears at the Maxwell-Ampere equation (assuming that the E-field from the electromagnet is low frequency? not sure I understand that part correctly). I also I am not familiar with the concept of opto-magnetic fluid.

Anyway I don't feel confident on working on this problem, I ll request for help from @Charles Link or @TSny that are both experts in classical EM.

It's a purely magnetostatic problem, so the extra term in Ampère's law can be ignored. This is such a tough problem, I have been working on it for almost three days and I still can't make any sense out of it.

 

[Charles Link]

The shell will only affect the y component, but one suggestion is to first work the problem without the shell. For the x component, there is no magnetic surface charges, (in the pole model of solving the magnetostatic problem), and you have $B_x=\mu_o H_{ox}+M_x$ where $M_x=\mu_o \chi_m H_{ox}$. $\\$ In the y direction you get magnetic surface charge density $\sigma_m=M_y \cdot \hat{n}$ that contributes (actually an opposite contribution) to the $H_y$, and I would need to work out the extra details if you include the shell. In the vacuum, the $H_{oy}$ is unchanged, because the layers of magnetic surface charges come in pairs that are opposites of each other. In the material, though, the effect is is reduce $H_{oy}$. $\\$ It should be noted that in the y-direction, it becomes a self-consistent problem, in computing the $H_y$'s in each region. In principle, it really isn't too much more difficult to solve with the shell, than to solve without it. It simply involves one more $H_y$ in the shell to solve for. The $H_y$ in the upper shell will be the same as the $H_y$ in the lower shell. (there of course is also the $M_y$ of the shell, and more magnetic surface charge layers to account for, so the algebra might get somewhat lengthy).

 

[phys194]

The shell will only affect the y component, but one suggestion is to first work the problem without the shell. For the x component, there is no magnetic surface charges, (in the pole model of solving the magnetostatic problem), and you have $B_x=\mu_o H_{ox}+M_x$ where $M_x=\mu_o \chi_m H_{ox}$. $\\$ In the y direction you get magnetic surface charge density $\sigma_m=M_y \cdot \hat{n}$ that contributes (actually an opposite contribution) to the $H_y$, and I would need to work out the extra details if you include the shell. In the vacuum, the $H_{oy}$ is unchanged, because the layers of magnetic surface charges come in pairs that are opposites of each other. In the material, though, the effect is is reduce $H_{oy}$. $\\$ It should be noted that in the y-direction, it becomes a self-consistent problem, in computing the $H_y$'s in each region. In principle, it really isn't too much more difficult to solve with the shell, than to solve without it. It simply involves one more $H_y$ in the shell to solve for. The $H_y$ in the upper shell will be the same as the $H_y$ in the lower shell. (there of course is also the $M_y$ of the shell, and more magnetic surface charge layers to account for, so the algebra might get somewhat lengthy).

 

[phys194]

My bad, the expression in the middle should have been $$A\cos(x)=\frac{-\mu_0H_0}{\sqrt{2} k \sinh(kh_2/2)}.$$ So, the last expression should change accordingly, but the general idea stays the same.

 

[Charles Link]

Unfortunately, we are not on the same page in the solution of this problem. For the x direction, the way I see the solution, it is very simple because there are no magnetic poles in the problem. The x direction solution is similar to that of a long cylindrical sample placed in a uniform magnetic field. With such a problem, they usually call it the z-axis, instead of the x direction. $\\$ Perhaps I am missing something, but your solution leaves me puzzled.

 

[Charles Link]

Upon working through the solution in the y-direction, there is actually a simple way of working it: We can assume $B_y$ is continuous and constant, so that $B_y=\mu_o H_{oy}=\mu_o H_{1y} +M_{1y}=\mu_o H_{2y}+M_{2y}$, etc.
Now $M_{1y}=\mu_o \chi_1 H_{y1}$, and $M_{2y}=\mu_o \chi_2 H_{2y}$. $\\$ Note: $\mu=\mu_o (1+ \chi)$.