Potential of a spherical shell

[Physicslearner500039]

Homework Statement

A thick spherical shell of charge Q and uniform volume charge density ρ is bounded by radii r1 and r2 > r1. With V = 0 at infinity, find the electric potential V as a function of distance r from the center of the distribution, considering regions (a) r > r2, (b) r2> r > r1 and (c) r < r1 (d) Do these solutions agree with each other at r = r2 and r = r1?

Relevant Equations

NA

a. This solution is i can consider the charge Q as a point charge and the electric potential at a distance r is
$V = Q/(4πεοr)$
b. This is where the confusion starts again when r2>r>r1, my answer

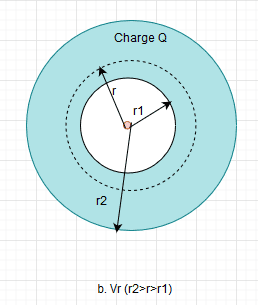
$V = ρ*4*π(r^3 - r_1^3)/(3*4πεοr) \\ V = ρ*(r^3-r_1^3)/3εοr;$
I know i am making some mistake as the answer does not match.

c. For r < r1, the potential should be 0. I know that for a conducting sphere the potential at the surface is equal to at the center and they are equi- potential surfaces. But in this case below r1 there is no surface hence the potential should be 0. Please advise.

 

[haruspex]

I know i am making some mistake as the answer does not match.

For r < r1, the potential should be 0

You are making the same mistake in both parts. There is no field inside a uniform spherical shell, but that only means the potential is constant. It does not mean the potential is zero.

 

[Physicslearner500039]

If i start from the basics

I want to calculate the potential at point P wrt ∞. The potential at ∞ is 0. $V_∞=0$
The standard equation is
$V_f - V_i = -\int_i^f \vec E .\vec {ds}$
Initial point is ∞ and the final point is p.
$V_∞ - V_p = -\int_p^∞ \vec E .\vec {ds}$
$0 - V_p = -\int_p^s \vec E .\vec {ds} -\int_s^∞ \vec E .\vec {ds}$
$V_p = \int_p^s \vec E .\vec {ds} + \int_s^∞ \vec E .\vec {ds}$
Let
$V_1 = \int_p^s \vec E .\vec {ds}$ and $V_2 = \int_s^∞ \vec E .\vec {ds}$
$V_p = V_1 + V_2$
$V_2$ is the potential on the surface with radius $r_2$ at the point $S$.
$V_2 = Q/4 \pi \epsilon r_2$

Calculation of potential $V_1$ is
Consider a point p at distance r the charge enclosed is
$q_{enc} = Q*(r^3/(r_2^3-r_1^3))$
The electric field is
$E = (Q*r^3)/(4\pi\epsilon*r^2*(r_2^3-r_1^3)) \\ E = (Q*r)/(4\pi\epsilon*(r_2^3-r_1^3))$

$V_1 = \int_{r_1}^{r_2} E dr \\ V_1 = \int_{r_1}^{r_2} (Q*r)/(4\pi\epsilon*(r_2^3-r_1^3))dr \\ V_1 = Q*(r_2^2 - r_1^2)/(8\pi\epsilon*(r_2^3-r_1^3))$
Please advise if i am in correct direction.

 

[hutchphd]

By definition your V₁ should depend explicitly on r. You have defined six different potentials V_something...just write them as V(r₁) etc or V(r) for r>r₂.
I do think you are going in the right direction generally.

 

[kuruman]

If i start from the basics

View attachment 261871
I want to calculate the potential at point P wrt ∞. The potential at ∞ is 0. $V_∞=0$
The standard equation is
$V_f - V_i = -\int_i^f \vec E .\vec {ds}$
Initial point is ∞ and the final point is p.
$V_∞ - V_p = -\int_p^∞ \vec E .\vec {ds}$

If the initial point is at infinity then you should write $V_p - V_{\infty} = -\int_{\infty}^p \vec E \cdot \vec {ds}$. This would change the sign.

$0 - V_p = -\int_p^s \vec E .\vec {ds} -\int_s^∞ \vec E .\vec {ds}$
$V_p = \int_p^s \vec E .\vec {ds} + \int_s^∞ \vec E .\vec {ds}$

Why do you find it necessary to introduce the intermediate point $s$? Just do the integral from infinity to $p$.

$\dots$
The electric field is
$E = (Q*r^3)/(4\pi\epsilon*r^2*(r_2^3-r_1^3)) \\ E = (Q*r)/(4\pi\epsilon*(r_2^3-r_1^3))$

This is incorrect; the electric field is not continuous at $r=r_2$. You need to rederive it from Gauss's law after you correct your expression for $q_{enc}$ which is the source of the error.

 

[haruspex]

The standard equation is
$V_f - V_i = -\int_i^f \vec E .\vec {ds}$

You are making it hard for yourself by bothering with fields. Just work with potentials, which are continuous.
What is the potential at the surface of a shell due to the charge on the shell?
What about inside the shell and outside the shell?
So what is the total potential at a point that is inside one set of shells and outside another set?

 

[Physicslearner500039]

If the initial point is at infinity then you should write $V_p - V_{\infty} = -\int_{\infty}^p \vec E \cdot \vec {ds}$. This would change the sign.

Yes it is my mistake

Why do you find it necessary to introduce the intermediate point $s$? Just do the integral from infinity to $p$.
This is incorrect; the electric field is not continuous at $r=r_2$. You need to rederive it from Gauss's law after you correct your expression for $q_{enc}$ which is the source of the error.

I removed it. The solution is

$V_r - V_\infty = -\int_\infty^{r} \vec E.\vec{ds}$
$V_r = -\int_\infty^{r_2} \vec E.\vec{ds} -\int_{r_2}^r \vec E.\vec{ds}$
The potential on the surface
$-\int_\infty^{r_2} \vec E.\vec{ds} = Q/4\pi\epsilon *r_2 = 4\rho\pi *(r_2^3 - r_1^3)/(3*4\pi\epsilon *r_2)$
$-\int_\infty^{r_2} \vec E.\vec{ds} =\rho(r_2^3 - r_1^3)/(3\epsilon r_2)$
$\rho/3\epsilon(r_2^2 - \frac {r_1^3} {r_2})$ ---> 1

To find the next potential applying the Gauss law to find the enclosed charge. Assuming a sphere at a radius x
$\int_{r_2}^r \rho * (x^3 - r_1^3){dx}/ 3\epsilon(r_2^3 - r_1^3)x^2$
$\rho/3\epsilon(r_2^3 - r_1^3)\int_{r_2}^r(x^3 - r_1^3){dx}/x^2$
$\rho/3\epsilon[\frac 1 2 x^2 + \frac {r_1^3} x]_{r_2}^r$
$\rho/3\epsilon(0.5r^2 +\frac {r_1^3} r - 0.5 r_2^2 - \frac {r_1^3} {r_2})$
The negative of the above expression is
$\rho/3\epsilon(-0.5r^2 -\frac {r_1^3} r + 0.5 r_2^2 + \frac {r_1^3} {r_2})$ ----> 2

Hence the net potential is adding equations 1 and 2 is
$\rho/3\epsilon(1.5r_2^2 - 0.5r^2 - \frac {r_1^3} r)$

 

[kuruman]

Yes it is my mistake

I removed it. The solution is
$V_r - V_\infty = -\int_\infty^{r} \vec E.\vec{ds}$
$V_r = -\int_\infty^{r_2} \vec E.\vec{ds} -\int_{r_2}^r \vec E.\vec{ds}$

I don't understand this. There are three regions in space where the potential is expressed by different functions, i.e. the potential is a piecewise continuous function. These are
Region 1, $(r \leq r_2$) where the electric field is $E_1$.
Region 2, $(r_1\leq r \leq r_2$) where the electric field is $E_2$.
Region 3, $(r \leq r_1$) where the electric field is $E_3$.
Your first equation defines $V_r$ as the potential is region 1, i.e. $V_1$, whilst your second equation defines $V_r$ as the potential in region 2, i.e. $V_2$. You cannot use the same symbol for two different entities without confusing yourself. Use separate symbols for the three separate potentials and electric fields.

You might wish to do the integrals with the correct electric fields in each region or consider @haruspex's suggestion in #8 for a more direct approach.