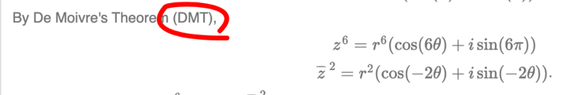Why Does the Complex Conjugate Involve Negating the Argument Theta?
- Context: Undergrad
- Thread starter Leo Liu
- Start date
Click For Summary
SUMMARY
The discussion centers on the mathematical concept of complex conjugates, specifically why negating the argument θ results in the conjugate of a complex number. The participants confirm that if z = re^{iθ}, then the conjugate is expressed as \(\bar{z} = re^{-iθ}\). This relationship is derived using Euler's Formula, \(e^{iθ} = \cos{θ} + i\sin{θ}\), and is validated through algebraic manipulation and double angle trigonometric identities. The importance of understanding these fundamentals is emphasized for anyone studying complex numbers.
PREREQUISITES- Understanding of complex numbers and their representation in polar form.
- Familiarity with Euler's Formula, \(e^{iθ} = \cos{θ} + i\sin{θ}\).
- Knowledge of trigonometric identities, particularly double angle formulas.
- Basic algebraic manipulation of complex expressions.
- Study the derivation and applications of Euler's Formula in complex analysis.
- Learn about the properties and applications of complex conjugates in various mathematical contexts.
- Explore trigonometric identities and their proofs, focusing on double angle formulas.
- Practice converting between rectangular and polar forms of complex numbers.
Students of mathematics, particularly those studying complex analysis, as well as educators and anyone seeking to deepen their understanding of complex numbers and their properties.
Similar threads
- · Replies 3 ·
- · Replies 7 ·
Undergrad
Complex numbers: reinventing the wheel?
- · Replies 12 ·
Undergrad
Qubits state calculation
- · Replies 6 ·
- · Replies 6 ·
Graduate
Rotations in the complex plane
- · Replies 2 ·
- · Replies 2 ·
- · Replies 2 ·
- · Replies 19 ·