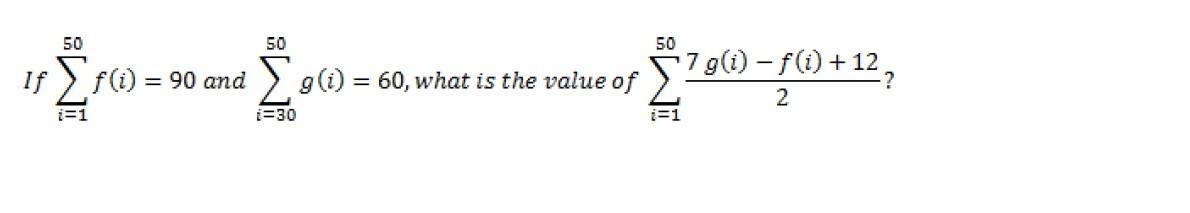Discussion Overview
The discussion revolves around evaluating a sigma notation expression in precalculus, specifically involving two functions, f and g, with given summation values. Participants explore the implications of these functions being constants and the calculations involved in deriving the final value.
Discussion Character
- Homework-related
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant presents a sigma notation problem and provides initial summation values for f and g.
- Another participant questions the definitions of f and g, suggesting they are implied constants.
- Some participants calculate a potential value of 465 based on assumed constant values for f and g.
- There is a suggestion that if f(i) and g(i) are constants, then g(i) could be calculated as 60/21.
- One participant points out that there is no need to assume f(i) and g(i) are constants and provides a detailed breakdown of the sigma notation calculation.
- Another participant acknowledges confusion regarding the indices for g(i) and suggests that the problem may not have a definite solution due to potential typographical errors in the original post.
Areas of Agreement / Disagreement
Participants express differing views on whether f(i) and g(i) should be treated as constants, and there is no consensus on the implications of the indices for g(i). The discussion remains unresolved regarding the correctness of the assumptions and calculations.
Contextual Notes
There are limitations regarding the assumptions made about the functions f and g, and the potential typographical error in the problem statement may affect the interpretation of the indices.