Precalculus: What is the value of this sigma notation?

[ukumure]

Hi, I'm currently a Grade 11 student and I need help for this question (Precalculus):

If $\sum\limits_{i=1}^{50} f(i)=90$ and $\sum\limits_{i=30}^{50} g(i)=60$, what is the value of $\sum\limits_{i=1}^{50} (7 g(i)-f(i)+12)/(2)$?

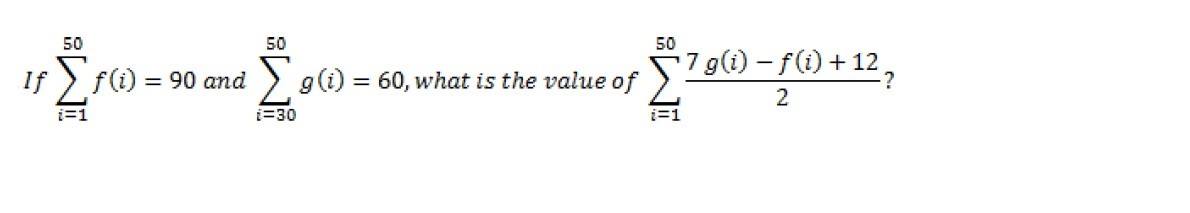
P.S. To those who could answer this, it would be a great help for me! Thank you so much!

 

[Greg]

Do you have definitions for [math]f[/math] and [math]g[/math]?

 

[Greg]

Oh! Those definitions are implied... :poop:

[math]f(i)=1.8.[/math] and [math]g(i)=1.2[/math] both suffice as definitions for [math]f,\,g[/math] if I am not mistaken... After a few basic calculations we may arrive at:

[math]\frac{420-90+600}{2}=465[/math]. Do you see that too?

Hint: use the fact that summation is associative and sum each addend separately with all operations being applied according to BEDMAS. Brackets around the numerator are omitted but in accordance with notational convention they are implied. The string

[math](7g(i)-f(i)+ 12)/2[/math] may be more useful to you.

 

[ukumure]

Oh! Those definitions are implied... :poop:

[math]f(i)=1.8.[/math] and [math]g(i)=1.2[/math] both suffice as definitions for [math]f,\,g[/math] if I am not mistaken... After a few basic calculations we may arrive at:

[math]\frac{420-90+600}{2}=465[/math]. Do you see that too?

Hint: use the fact that summation is associative and sum each addend separately with all operations being applied according to BEDMAS. Brackets around the numerator are omitted but in accordance with notational convention they are implied. The string

[math](7g(i)-f(i)+ 12)/2[/math] may be more useful to you.

Thank you so much for helping me! This means a lot to me! Thank you!

 

[skeeter]

Oh! Those definitions are implied... :poop:

[math]f(i)=1.8.[/math] and [math]g(i)=1.2[/math] both suffice as definitions for [math]f,\,g[/math] ...

If the assumption that both $f(i)$ and $g(i)$ are constants is correct, wouldn’t

$g(i) = \dfrac{60}{21}$ ?

 

[Greg]

If the assumption that both $f(i)$ and $g(i)$ are constants is correct, wouldn’t

$g(i) = \dfrac{60}{21}$ ?

Yes, I agree. My error was missing [math]i[/math] = 30 and assuming [math]i[/math] = 1 .

 

[Opalg]

If the assumption that both $f(i)$ and $g(i)$ are constants is correct, wouldn’t

$g(i) = \dfrac{60}{21}$ ?

There is no need to assume that $f(i)$ and $g(i)$ are constants. You just need to use the fact that $$ \sum_{i=1}^{50} \frac{7 g(i)-f(i)+12}2 = \frac12\sum_{i=1}^{50} (7 g(i)-f(i)+12) = \frac12\left(7\sum_{i=1}^{50}g(i) - \sum_{i=1}^{50}f(i) + \sum_{i=1}^{50}12\right) = \frac12(7*60 - 90 + 600) = 465.$$

 

[skeeter]

There is no need to assume that $f(i)$ and $g(i)$ are constants. You just need to use the fact that $$ \sum_{i=1}^{50} \frac{7 g(i)-f(i)+12}2 = \frac12\sum_{i=1}^{50} (7 g(i)-f(i)+12) = \frac12\left(7\sum_{i=1}^{50}g(i) - \sum_{i=1}^{50}f(i) + \sum_{i=1}^{50}12\right) = \frac12(7*60 - 90 + 600) = 465.$$

take another look at the indices for g(i) in the original post ...

 

[Opalg]

take another look at the indices for g(i) in the original post ...

I should have looked more closely! As stated, the problem can have no definite solution.

 

[ukumure]

take another look at the indices for g(i) in the original post ...

I got confused at the problem, especially the given i=30. But the instructor told me it was a typographical error. Thank you so much for your help! <3

 

[HOI]

Aaargh!