Primitive Elements and Free Modules .... ....

[Math Amateur]

I am reading Paul E. Bland's book, "Rings and Their Modules".

I am focused on Section 4.3: Modules Over Principal Ideal Domains ... and I need some help in order to fully understand the proof of Proposition 4.3.14 ... ...

Proposition 4.3.14 reads as follows:

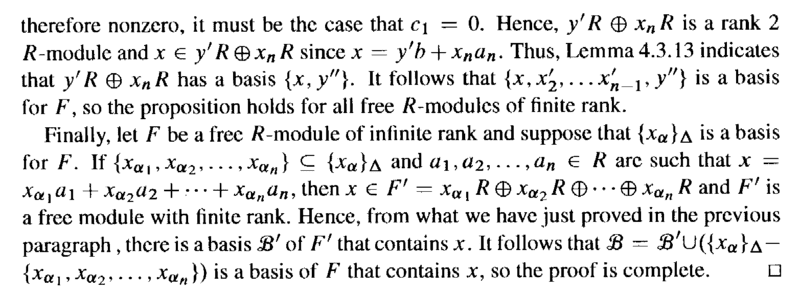In the above proof by Bland we read the following:

" ... ... The induction hypothesis gives a basis $\{ x, x'_2, \ ... \ ... \ x'_{n -1} \}$ of $M$ and it follows that $\{ x, x'_2, \ ... \ ... \ x'_{n - 1}, x'_n \}$ is a basis of $F$ that contains $x$ ... ... "My question is as follows:

Why/how exactly does it follow that $\{ x, x'_2, \ ... \ ... \ x'_{n - 1}, x'_n \}$ is a basis of $F$ that contains $x$. ... ...Help will be appreciated ...

Peter====================================================================================================

It may help PFmembers reading this post to have access to Bland's definition of 'primitive element of a module' ... especially as it seems to me that the definition is a bit unusual ... so I am providing the same as follows:

Hope that helps ... ...

Peter

 

[andrewkirk]

That $\{x_1,...,x_n\}$ is a basis for $F$ means the same as that
$$F=x_1R\oplus...\oplus x_nR$$
and since $M\triangleq x_1R\oplus...\oplus x_{n-1}R$ we have $F=M\oplus x_nR$.

Since the induction hypothesis gives us that $\{x, x'_2,...,x'_{n-1}\}$ is a basis of $M$ we have
$$M = xR\oplus x'_2R\oplus x'_3R\oplus...\oplus x'_{n-1}$$
So we have
$$F=M\oplus x_nR
= xR\oplus x'_2R\oplus x'_3R\oplus...\oplus x'_{n-1}\oplus x_nR$$
which is equivalent to saying that $\{x,x'_2,...,x'_{n-1},x_n\}$ is a basis for $F$.

 

[Math Amateur]

Thanks Andrew ...

Appreciate your help ...

Peter