Probability density for observable with continuous Spectrum

[Naarogaut]

I'm given a wave function for an electron which is given as:

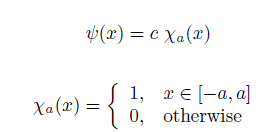
For an electron in this state the kinetic energy is being measured, where the kinetic energy operator is p^2/2m. How can I find the probability (density) that an electron is found to have kinetic energy in the interval [E, E+dE]? I was thinking about using the born rule, but I am struggeling to use it for the infinite dimensional Hilbert space, since the eigenstates of the kinetic energy operator degenerate as far as I can tell...

 

[DrClaude]

How about calculating $\psi(p)$?