SUMMARY
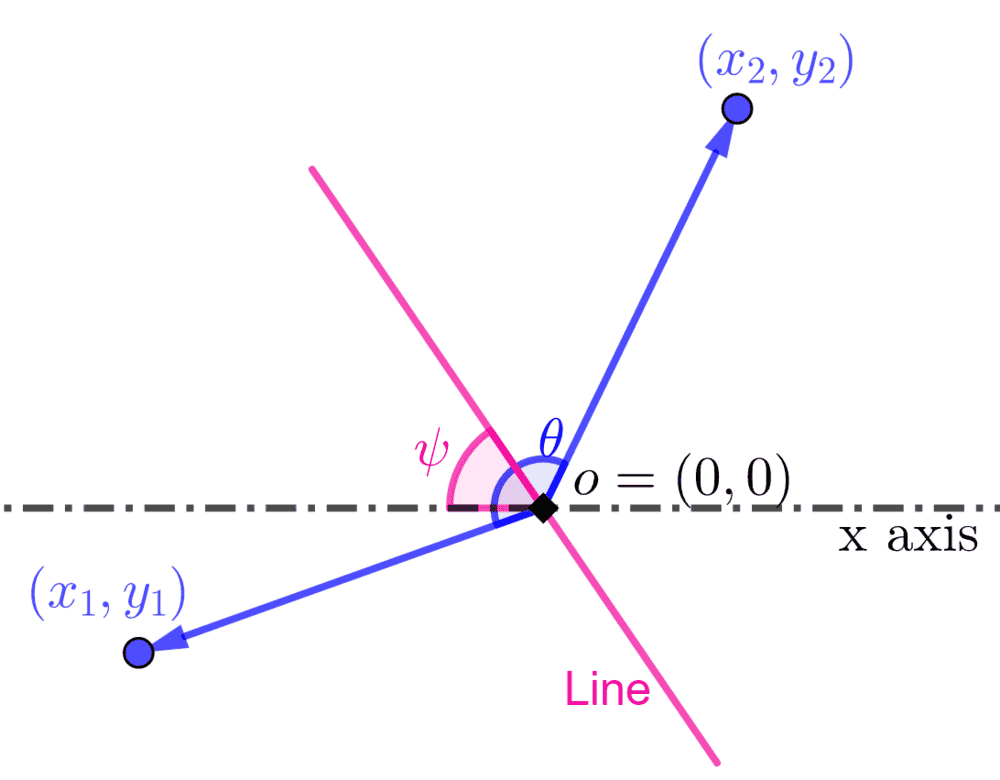
The discussion focuses on calculating the probability that two points, represented as ($x_1, y_1$) and ($x_2, y_2$), lie on opposite sides of a line through the origin that makes an angle $\psi$, uniformly distributed in $[0, \pi]$, with the x-axis. The angle between the two points is denoted as $\theta$, which has a probability density function $f_{\theta}(\rho)$ for $\theta \in (0, 2\pi)$. Key insights include that if $\theta$ is uniformly distributed between $0$ and $2\pi$, the points will be on opposite sides of the line half the time, leading to a probability of $\theta/\pi$ for a fixed $\theta$. The discussion emphasizes the need for clarity in problem definition and notation.
PREREQUISITES
- Understanding of probability density functions, specifically $f_{\theta}(\rho)$.
- Familiarity with angles and their distributions, particularly uniform distributions.
- Basic knowledge of geometric concepts related to lines and points in a Cartesian plane.
- Proficiency in using LaTeX for mathematical notation.
NEXT STEPS
- Explore the implications of uniform distributions in probability theory.
- Learn about the properties of angles in geometry, particularly in relation to Cartesian coordinates.
- Study the application of probability density functions in real-world scenarios.
- Investigate the use of LaTeX for mathematical expressions and its best practices.
USEFUL FOR
This discussion is beneficial for mathematicians, statisticians, physics students, and anyone interested in probability theory and geometric analysis. It is particularly relevant for those working with angular distributions and probability density functions.