Problem dealing with Position and Velocity

[mathwhiz]

Homework Statement

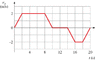
You are consulting for an elevator company. During a safety test, technicians created the following graph of the velocity of the elevator versus time; you have been asked to interpret the graph. Unfortunately, you are told that the technician who printed the graph has made two mistakes. The labeled interval on the velocity axis should be 2.5 m/s rather than 2.0 m/s, and the labeled time interval should be 3.6 s rather than 4.0 s. You should begin by redrawing the graph on your own paper with the proper labels on the velocity and time axes.

Since this motion is purely one-dimensional, give your answers to the following questions using a coordinate system consisting of a y-axis in the Up-Down direction with Up as positive. Indicate directions by the appropriate plus or minus sign. Assume that the test begins (at time zero) with the elevator at position y0=-3.2 m (i.e. 3.2 meters below ground level -- ground level has been selected as the location at which y=0).

(a) What is the position of the elevator at time 1.8 seconds?
(b) What is the position of the elevator at time 7.2 seconds?

Homework Equations

$X_f = x_0 + V_x(ΔT)$

Maybe $v = d/ΔT$

$v_x = Δx/Δt$

The Attempt at a Solution

Attempt 1:

Just plug everything in, $v_x = v_xavg = v$ so $v_x = 1.389 m/s$
$x_f = -3.2m + 1.389m/s(1.8s)$
$x_f = -0.7m$ WRONG!

Attempt 2:

Tried to multiply by the velocity at time 1.8s according to my redrawn graph, which was 2.5
$x_f = -3.2m + 2.5m/s * 1.8s$
$x_f = 1.3m$ WRONG ONCE AGAIN!

Attempt 3:

Tried to plug my numbers into a similar problem someone asked about on this forum
$v_x = -3.2 + (2.5/1.8) * 1.8$ I don't even know but it was wrong again.
I just would like some guidance on what I need to be looking at because obviously my way is wrong.
I'm going to attach the original graph, and my redrawn graph.

 

[voko]

How can you describe the motion in the first 1.8 seconds? Is it uniform? Or uniformly accelerated? Something else? How do you find displacement for this kind of motion? How do you find displacement if you are given the graph of velocity vs time in general?

 

[mathwhiz]

The motion in the first 1.8 seconds is uniform. So I know from there that velocity = average velocity which in turn equals the speed. As far as displacement it will be the distance from 0 secs to 1.8 seconds


$Δx = \sqrt{(1.8)^2 +(2.5)^2}$
$Δx = 3.08m$

so should I just do
$x_f=-3.21 + 3.08$
$= -0.13$

 

[voko]

If velocity = average velocity, then velocity must not change. However, it is seen from the graph that it does change during the first 1.8 seconds.

 

[mathwhiz]

Of course, I have to remember a slope like that means constant if it were a position vs time graph which this is not. This is obviously velocity vs time.
$V_x @ 1.8s = 2.5 m/s$
so why can't I just plug it into $x_f = x_i+v_x*Δt$ and get the correct number.

Now, I think I need to find $V_avg$ multiply that by $Δt$ then add whatever number I get to the original starting point of the elevator at -3.2m.

so my formula would look something like:

and I believe that is the exact formula I saw on the previous post

$X_f = -3.2 + (2.5/1.8) * 1.8$

 

[mathwhiz]

Ahhhh no that's not right I tried that on attempt 1 already

 

[Tanya Sharma]

Mathwiz...since the graph between time t=0 and t=1.8 is a straight line ,it means the object is having uniform acceleration .You can find the acceleration by taking any two points on the line and using a=Δv/Δt .

Then since the acceleration is constant , y = y₀+v₀t+(1/2)at².