Problem With a Slewing Bearing Crane

[Herbid]

Dear All Masters

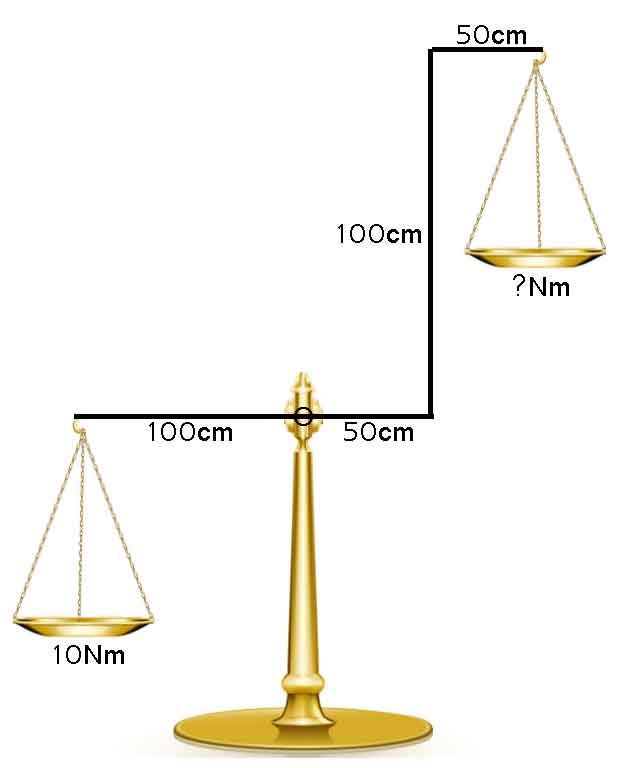
I have problem with slewing bearing crane.

My subcon made a crane that have a very high platform deck form slewing bearing.

They said it is fine and the height is not an issue as it is in lower place.

I know the higher the load from slewing bearing,
the bigger the force or moment works on it, especially in radial force,
like my pic attach.

But I don't know how to calculate the increasing of a radial force / moment that works physically.

Anyone can help?

Thanks.

 

[Baluncore]

Vertical forces are balanced when ? Nm = 10 Nm

 

[Herbid]

But a radial force is bigger than if the scale of left right load is a horizontal straight and same length of line.

 

[Baluncore]

You appear to be loading the system with vertical forces only.
If that is the case, the radial forces will be zero.
What radial forces are you considering.

 

[Herbid]

So if the vertical mast is higher than 100cm, let say as extreme as 1000cm (the weight is neglected),
it is still no radial forces acting to the right side of the hinge?

 

[Baluncore]

So if the vertical mast is higher than 100cm, let say as extreme as 1000cm (the weight is neglected), it is still no radial forces acting to the right side of the hinge?

If the forces are vertical, or due only to gravity, then the moment applied at the slew bearing is only the horizontal distance from the bearing vertical axis, multiplied by the weight hanging at that point.

 

[Nik_2213]

Don't forget snatch-loads and wind effects. A gust, micro-burst or partial sling failure may produce very, very large 'impulse' forces.

Um, there used to be a cautionary website documenting such civ-eng mishaps and mayhem, but it lost its server...

 

[Herbid]

Ok case closed.

I just wonder from this picture:

Is Tension in rope T, the same for hanging an anvil at Bottom Right (A),
or if we put it on Top Right? (B).

The hinge or fulcrum slightly off center to the left side.

Because now we have weight of big blue box.
is the center of gravity taking into account?

The blue box and black base is welded.

 

[Baluncore]

If the box is free to rotate about the fulcrum then T will be independent of the vertical position, A or B. It is the relative horizontal position that is important for balance.

The blue box and black base is welded.

What is welded to what?

 

[Herbid]

Understand.
Blue box is welded to black base, or blue and black is a one single unit device.

Now if there is a 100N horizontal force acting to blue box in top left side like pic attach:

Is Tension of Red Rope (T) the same for A and B condition?

 

[Baluncore]

You must learn to convert all the forces to x and y force components, at specified positions in space. Then you can work out the sum of all moments about the fulcrum and find the tension in the red rope.

 

[Herbid]

You must learn to convert all the forces to x and y force components, at specified positions in space. Then you can work out the sum of all moments about the fulcrum and find the tension in the red rope.

I see.
I think B will create much bigger tension in T since its center gravity position is farther away (result as a moment?) from fulcrum than A.

 

[Baluncore]

Your picture needs to be made into a diagram.
Start by defining the origin of (x=0,y=0) coordinates at the fulcrum.
Then specify the (x,y) position of attachments for the applied loads = forces.
Next resolve those forces into Fx and Fy components, which should be simple in this case.
Calculate the resultant moments at the fulcrum.
That will give you the tension in the tie.

 

[Herbid]

Your picture needs to be made into a diagram.
Start by defining the origin of (x=0,y=0) coordinates at the fulcrum.
Then specify the (x,y) position of attachments for the applied loads = forces.
Next resolve those forces into Fx and Fy components, which should be simple in this case.
Calculate the resultant moments at the fulcrum.
That will give you the tension in the tie.

I am about to start, but stuck when a center of gravity (mass?) is involved.

 

[tech99]

A good method for analysing these problems is to,
Resolve all vertical force componets
Resolve all horizontal components
Take moments about any vertical axis.
Then you have three simultaneous equations which are easily solved.

 

[Herbid]

My calculation for B.I assume an extreme condition that the center of gravity is right bellow 1 ton anvil (for easier cal).
So I draw straight line as a lever from fulcrum to the that center.

Skiip.
The total moment Inertia is:
Inertia of 1 Ton anvil plus (100N x cos a) x length of red lever.

Then Tension force in T is:
Moment in Red divide to length of black's lever.