- #1
John Duffield
- 11
- 1
I've been discussing this elsewhere recently. In my opinion Purcell's explanation in section 5.9 doesn't actually explain why an electron moves in a circular or helical fashion in a magnetic field:
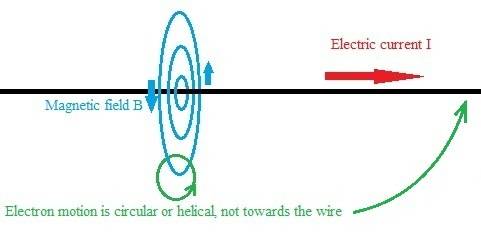
However this length-contraction explanation has been around for so long that's it's rather taken for granted.
However this length-contraction explanation has been around for so long that's it's rather taken for granted.