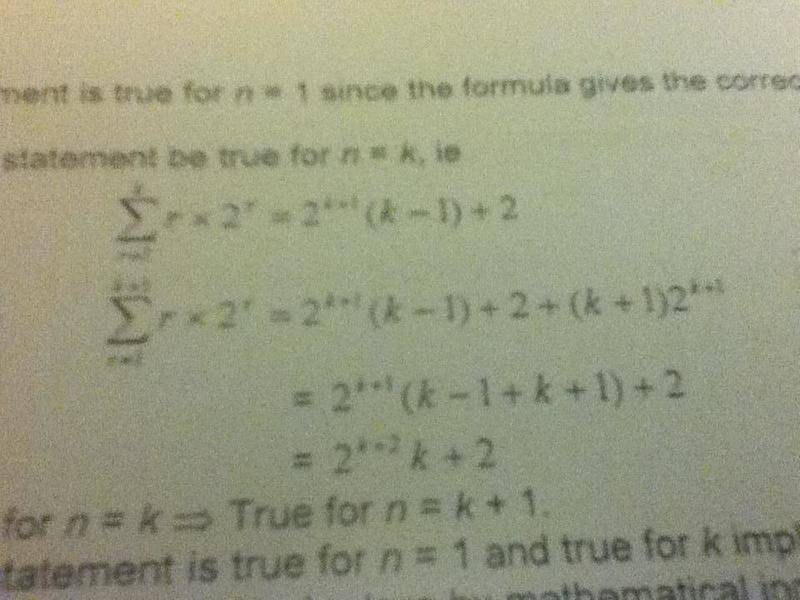SUMMARY
The discussion centers on understanding the transition from the expression 2^(k+1) to 2^(k+2) in a proof by induction context. The key insight is that multiplying 2^(k+1) by 2 effectively raises the exponent by 1, resulting in 2^(k+2). The mathematical manipulation involves recognizing that 2^(k+1) multiplied by (k-1+k+1) simplifies to 2^(k+2)k, confirming the validity of the induction step.
PREREQUISITES
- Understanding of mathematical induction
- Familiarity with exponent rules
- Basic algebraic manipulation skills
- Knowledge of sequences and series
NEXT STEPS
- Study mathematical induction proofs in detail
- Learn about exponentiation rules and properties
- Explore common induction problems and solutions
- Review algebraic techniques for simplifying expressions
USEFUL FOR
Students of mathematics, educators teaching proof techniques, and anyone interested in enhancing their problem-solving skills in algebra and induction.