Happiness
- 686
- 30
I want to prove that the transformation equation for electric field holds, namely Ex = Ex', where Ex is the x component of E field in S frame and Ex' is that in S' frame, for the special case in which the charged particle has a vertical velocity Uy' in the S' frame (Ux' = Uz' = 0). It is already proven in the textbook by Robert that the transformation equations (4-5) for Ex, Ey and Ez holds for the special case in which the charged particle is at rest in S' frame (U' = 0).
Equations (4-5) are
## E^\prime_x = E_x ##
## E^\prime_y = \gamma(E_y - vB_z)##
## E^\prime_z = \gamma(E_z + vB_y)##
My approach is to have an S'' frame moving with respect to S' frame at V' = Uy' so that the charged particle is at rest in S'' frame. (S' frame is moving in the x direction at V with respect to S frame, while S'' frame is moving in the y direction with respect to S' frame.) Then I could use equations (4-5) to find E'' from E', and then use equations (4-5) again to find E from E'', hence relating E to E'. Since E'' is the frame the charged particle is at rest, equations (4-5) holds.
My result is that Ex and Ex' are not equal, contrary to the claim that equations (4-5) hold in general for any velocity of the charged particle.
Background reading: Introduction to Special Relativity by Robert Resnick (Wiley 1968) Page 163-165
My result:
By Equations (4-5) and considering ##S^{\prime\prime}## and ##S^{\prime}##,
## E^{\prime\prime}_x = \gamma^\prime(E^\prime_x+v^\prime B^\prime_z) ##
## E^{\prime\prime}_y = E^\prime_y ##
## E^{\prime\prime}_z = \gamma^\prime(E^\prime_z-v^\prime B^\prime_x) ##
Let ## v_0 ## be the velocity ## S^{\prime\prime} ## moves with respect to S, and ## \theta ## be the angle ## v_0 ## makes from the ##x## axis.
Let ## x_0 ## be the axis that points in the direction of ## v_0 ##, and ## y_0 ## be the axis that is ## 90^\circ ## anticlockwise from ## x_0 ##.
## E^{\prime\prime}_{x_0} = \gamma^\prime\cos\theta\ (E^\prime_x+v^\prime B^\prime_z)+\sin\theta\ E^\prime_y ##
## E^{\prime\prime}_{y_0} = -\gamma^\prime\sin\theta\ (E^\prime_x+v^\prime B^\prime_z)+\cos\theta\ E^\prime_y ##
## E^{\prime\prime}_{z_0} = \gamma^\prime(E^\prime_z-v^\prime B^\prime_x) ##
By Equations (4-5) and considering ##S## and ##S^{\prime\prime}##,
## E_{x_0} = E^{\prime\prime}_{x_0} = \gamma^\prime\cos\theta\ (E^\prime_x+v^\prime B^\prime_z)+\sin\theta\ E^\prime_y ##
## E_{y_0} = \gamma_0(E^{\prime\prime}_{y_0}+v_0B^{\prime\prime}_{z_0}) = -\gamma_0\gamma^\prime\sin\theta\ (E^\prime_x+v^\prime B^\prime_z)+\gamma_0\cos\theta\ E^\prime_y+\gamma_0v_0B^{\prime\prime}_{z_0} ##
## E_{z_0} = \gamma_0(E^{\prime\prime}_{z_0}-v_0B^{\prime\prime}_{y_0}) = \gamma_0\gamma^\prime(E^\prime_z-v^\prime B^\prime_x)-\gamma_0v_0B^{\prime\prime}_{y_0} ##
## E_x = E_{x_0}\cos\theta-E_{y_0}\sin\theta = \gamma^\prime(\cos^2\theta+\gamma_0\sin^2\theta)(E^\prime_x+v^\prime B^\prime_z)+(1-\gamma_0)\sin\theta\cos\theta\ E^\prime_y-\gamma_0\sin\theta\ v_0B^{\prime\prime}_{z_0} \neq E^\prime_x ##
Handwritten result in more details:

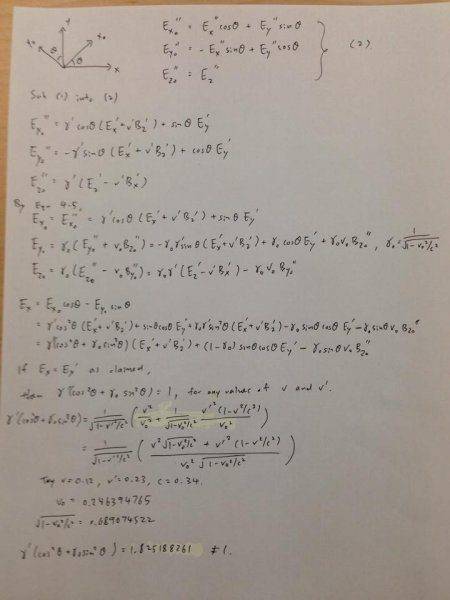
Equations (4-5) are
## E^\prime_x = E_x ##
## E^\prime_y = \gamma(E_y - vB_z)##
## E^\prime_z = \gamma(E_z + vB_y)##
My approach is to have an S'' frame moving with respect to S' frame at V' = Uy' so that the charged particle is at rest in S'' frame. (S' frame is moving in the x direction at V with respect to S frame, while S'' frame is moving in the y direction with respect to S' frame.) Then I could use equations (4-5) to find E'' from E', and then use equations (4-5) again to find E from E'', hence relating E to E'. Since E'' is the frame the charged particle is at rest, equations (4-5) holds.
My result is that Ex and Ex' are not equal, contrary to the claim that equations (4-5) hold in general for any velocity of the charged particle.
Background reading: Introduction to Special Relativity by Robert Resnick (Wiley 1968) Page 163-165
My result:
By Equations (4-5) and considering ##S^{\prime\prime}## and ##S^{\prime}##,
## E^{\prime\prime}_x = \gamma^\prime(E^\prime_x+v^\prime B^\prime_z) ##
## E^{\prime\prime}_y = E^\prime_y ##
## E^{\prime\prime}_z = \gamma^\prime(E^\prime_z-v^\prime B^\prime_x) ##
Let ## v_0 ## be the velocity ## S^{\prime\prime} ## moves with respect to S, and ## \theta ## be the angle ## v_0 ## makes from the ##x## axis.
Let ## x_0 ## be the axis that points in the direction of ## v_0 ##, and ## y_0 ## be the axis that is ## 90^\circ ## anticlockwise from ## x_0 ##.
## E^{\prime\prime}_{x_0} = \gamma^\prime\cos\theta\ (E^\prime_x+v^\prime B^\prime_z)+\sin\theta\ E^\prime_y ##
## E^{\prime\prime}_{y_0} = -\gamma^\prime\sin\theta\ (E^\prime_x+v^\prime B^\prime_z)+\cos\theta\ E^\prime_y ##
## E^{\prime\prime}_{z_0} = \gamma^\prime(E^\prime_z-v^\prime B^\prime_x) ##
By Equations (4-5) and considering ##S## and ##S^{\prime\prime}##,
## E_{x_0} = E^{\prime\prime}_{x_0} = \gamma^\prime\cos\theta\ (E^\prime_x+v^\prime B^\prime_z)+\sin\theta\ E^\prime_y ##
## E_{y_0} = \gamma_0(E^{\prime\prime}_{y_0}+v_0B^{\prime\prime}_{z_0}) = -\gamma_0\gamma^\prime\sin\theta\ (E^\prime_x+v^\prime B^\prime_z)+\gamma_0\cos\theta\ E^\prime_y+\gamma_0v_0B^{\prime\prime}_{z_0} ##
## E_{z_0} = \gamma_0(E^{\prime\prime}_{z_0}-v_0B^{\prime\prime}_{y_0}) = \gamma_0\gamma^\prime(E^\prime_z-v^\prime B^\prime_x)-\gamma_0v_0B^{\prime\prime}_{y_0} ##
## E_x = E_{x_0}\cos\theta-E_{y_0}\sin\theta = \gamma^\prime(\cos^2\theta+\gamma_0\sin^2\theta)(E^\prime_x+v^\prime B^\prime_z)+(1-\gamma_0)\sin\theta\cos\theta\ E^\prime_y-\gamma_0\sin\theta\ v_0B^{\prime\prime}_{z_0} \neq E^\prime_x ##
Handwritten result in more details:
Last edited: