- #1
Verne42
- 3
- 0
I have been learning SR from various sources. Most of the time from Feyman's Lectures but that's not the only place.
In II_26 he gives the transformation for the E-field of a moving charge in the x direction under a standard Lorentz configuration. In Eqn 26.11 he derives a formula for the Ex strength (at the x coordinate of a point to the right of the charge as observed in the stationary frame which sees the E-field moving) and states the strength is reduced by 1/gamma compared to what the strength would be as seen by the frame of the charge, (that is, E'x.) This derivation came by first transforming the potentials, and then taking derivatives.
Then later, in Sec 26-3 he does a different sort of derivation where he derives the E-field transformations directly from the E fields themselves. That is, he derives the relationship between E and E'. He arrives at the formulas given in Table 26.2 which clearly show that the primed and unprimed versions of the E-field in the x direction are equal. That is, Ex = E'x.
A double-take ensues. Are the two versions of the E field in the x direction equal or not? Eqn 26.11 says no. Table 26-2 says yes. I suspect it's some kind of misunderstanding about the coordinates being used. For example, in the Table26-2 equation for Efield transform Ex = E'x, is it really implying Ex(x, y, z, t) = E'x(x', y', x', t'). I assume that's what it means, yet Eqn 26.11 is not giving it that way, it's saying Ex(x, y, z, t) = blahblah(x, y, z, t). In other words, no primed coordinates on either side. Is that the discrepancy between the two formulas?
I've spent a lot of time going over this material, and admit I don't fully understand the 4-vector stuff though I get the gist of it. And I suspect the aforementioned usages of coordinates is the cause of my confusion. I concocted a diagram that illustrates the E field in both frames of reference (2D only), for an arbitrary amount of squishiness (read: velocity of the charge) and I look at the value of the E-field strength at an arbitrary point on the X-axis and give that strength a value of 17 V/m just because I like the number (it's made up, in other words). I wanted to visually see how it tracks between the two frames of reference. I do the same thing in the Y direction, picking a point on the equipotential line of the first point.
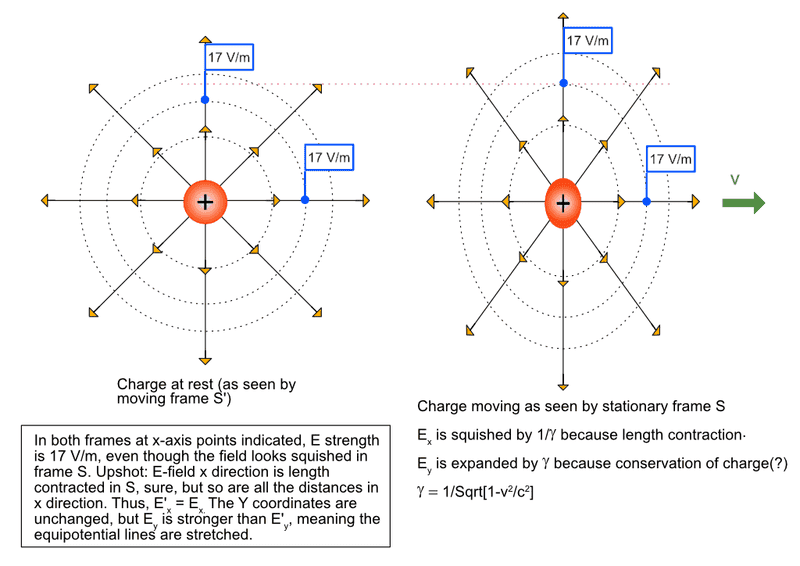
Does this diagram show things correctly? To wit:
(1) Are the equipotential lines on the squished E-field correctly proportioned?
(2) I (presumably) understand how the x direction is getting squished. Just plain ol' length contraction. But why is the Y direction expanded? Yes, I know it's due to the 4-vector transformations, but that doesn't really explain it. In fact, I can't find anywhere on the web, in books, etc., where this is explained, even though many places say that it happens. UPDATE: I see Feynman says in the same chapter that it's something to do with the ratio of the energy of the particle to its rest mass -- don't know how I missed that. My intuition on the diagram -- before I saw the Feynman statement -- says that it's due to a conservation of charge thing, kind of like squeezing a ball laterally and having the transverse sides pop out, aka conservation of volume on the part of the ball. Is this a good intuition? Does it roughly fit with Feynman's statement? Is it conservation of charge or conservation of the charge's momentum? Why doesn't anyone (besides Feynman in one short sentence) talk about this? Is it given in lectures and just not preserved in books and web articles? I unfortunately was never privy to such lectures when in undergrad and grad school in mechanical engineering way back in the 70s and 80s.
3) This stretching of the Y direction is implying that if a test charge were placed vertically above the moving charge, and that test charge was moving with same velocity, that from the stationary frame's point of view, the test charge would feel an extra upward force, beyond what Coulomb's law would say given their vertical distance. And that this is in addition to a magnetic force which ends up being directed downward. I assume that in general, these two additional effects do not entirely cancel. Is all of this correct?
Thanks for any help. I hope I explained the problem clearly enough.
In II_26 he gives the transformation for the E-field of a moving charge in the x direction under a standard Lorentz configuration. In Eqn 26.11 he derives a formula for the Ex strength (at the x coordinate of a point to the right of the charge as observed in the stationary frame which sees the E-field moving) and states the strength is reduced by 1/gamma compared to what the strength would be as seen by the frame of the charge, (that is, E'x.) This derivation came by first transforming the potentials, and then taking derivatives.
Then later, in Sec 26-3 he does a different sort of derivation where he derives the E-field transformations directly from the E fields themselves. That is, he derives the relationship between E and E'. He arrives at the formulas given in Table 26.2 which clearly show that the primed and unprimed versions of the E-field in the x direction are equal. That is, Ex = E'x.
A double-take ensues. Are the two versions of the E field in the x direction equal or not? Eqn 26.11 says no. Table 26-2 says yes. I suspect it's some kind of misunderstanding about the coordinates being used. For example, in the Table26-2 equation for Efield transform Ex = E'x, is it really implying Ex(x, y, z, t) = E'x(x', y', x', t'). I assume that's what it means, yet Eqn 26.11 is not giving it that way, it's saying Ex(x, y, z, t) = blahblah(x, y, z, t). In other words, no primed coordinates on either side. Is that the discrepancy between the two formulas?
I've spent a lot of time going over this material, and admit I don't fully understand the 4-vector stuff though I get the gist of it. And I suspect the aforementioned usages of coordinates is the cause of my confusion. I concocted a diagram that illustrates the E field in both frames of reference (2D only), for an arbitrary amount of squishiness (read: velocity of the charge) and I look at the value of the E-field strength at an arbitrary point on the X-axis and give that strength a value of 17 V/m just because I like the number (it's made up, in other words). I wanted to visually see how it tracks between the two frames of reference. I do the same thing in the Y direction, picking a point on the equipotential line of the first point.
Does this diagram show things correctly? To wit:
(1) Are the equipotential lines on the squished E-field correctly proportioned?
(2) I (presumably) understand how the x direction is getting squished. Just plain ol' length contraction. But why is the Y direction expanded? Yes, I know it's due to the 4-vector transformations, but that doesn't really explain it. In fact, I can't find anywhere on the web, in books, etc., where this is explained, even though many places say that it happens. UPDATE: I see Feynman says in the same chapter that it's something to do with the ratio of the energy of the particle to its rest mass -- don't know how I missed that. My intuition on the diagram -- before I saw the Feynman statement -- says that it's due to a conservation of charge thing, kind of like squeezing a ball laterally and having the transverse sides pop out, aka conservation of volume on the part of the ball. Is this a good intuition? Does it roughly fit with Feynman's statement? Is it conservation of charge or conservation of the charge's momentum? Why doesn't anyone (besides Feynman in one short sentence) talk about this? Is it given in lectures and just not preserved in books and web articles? I unfortunately was never privy to such lectures when in undergrad and grad school in mechanical engineering way back in the 70s and 80s.
3) This stretching of the Y direction is implying that if a test charge were placed vertically above the moving charge, and that test charge was moving with same velocity, that from the stationary frame's point of view, the test charge would feel an extra upward force, beyond what Coulomb's law would say given their vertical distance. And that this is in addition to a magnetic force which ends up being directed downward. I assume that in general, these two additional effects do not entirely cancel. Is all of this correct?
Thanks for any help. I hope I explained the problem clearly enough.
