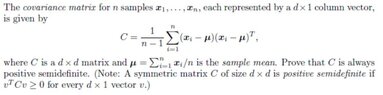AlanTuring
- 6
- 0
Hello,
i am having a hard time understanding the proof that a covariance matrix is "positive semidefinite" ...
i found a numbe of different proofs on the web, but they are all far too complicated / and/ or not enogh detailed for me.
View attachment 3290
Such as in the last anser of the link :
probability - What is the proof that covariance matrices are always semi-definite? - Mathematics Stack Exchange
(last answer, in particular i don't understad how they can passe from an expression
E{u T (x−x ¯ )(x−x ¯ ) T u}
to
E{s^2 }
... from where does thes s^2 "magically" appear ?
;)
i am having a hard time understanding the proof that a covariance matrix is "positive semidefinite" ...
i found a numbe of different proofs on the web, but they are all far too complicated / and/ or not enogh detailed for me.
View attachment 3290
Such as in the last anser of the link :
probability - What is the proof that covariance matrices are always semi-definite? - Mathematics Stack Exchange
(last answer, in particular i don't understad how they can passe from an expression
E{u T (x−x ¯ )(x−x ¯ ) T u}
to
E{s^2 }
... from where does thes s^2 "magically" appear ?
;)