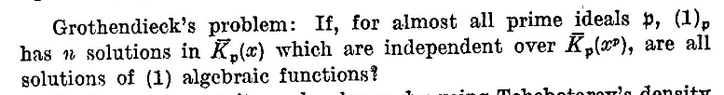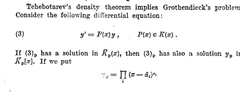Proof that the solutions are algebraic functions

[mathmari]

Hey!

I am looking at the following:

View attachment 5008

View attachment 5009

View attachment 5010 View attachment 5011

View attachment 5012 I haven't really understood the proof...

Why do we consider the differential equation $y'=P(x)y$ ? (Wondering)

Why does the sentence: "If $(3)_{\mathfrak{p}}$ has a solution in $\overline{K}_{\mathfrak{p}}(x)$, then $(3)_{\mathfrak{p}}$ has also a solution $y_{\mathfrak{p}}$ in $\overline{K}_{\mathfrak{p}}[x]$." stand? (Wondering)

 

[mathmari]

Why do we consider the differential equation $y'=P(x)y$ ?

Since the proof for Grothedieck's problem stands for $n=1$, we consider a differential equation of the form $\alpha_0(x)y'+\alpha_1(x) y=0, \alpha_i(x)\in K[x]$.
So $\alpha_0(x)y'+\alpha_1 (x) y=0 \Rightarrow \alpha_0(x)y'=-\alpha_1(x)y \Rightarrow y'=P(x)y$, where $P(x)=-\frac{\alpha_1(x)}{\alpha_0(x)}\in K(x)$.

Is this correct? (Wondering)

Why does the sentence: "If $(3)_{\mathfrak{p}}$ has a solution in $\overline{K}_{\mathfrak{p}}(x)$, then $(3)_{\mathfrak{p}}$ has also a solution $y_{\mathfrak{p}}$ in $\overline{K}_{\mathfrak{p}}[x]$." stand? (Wondering)

$\overline{K}$ is the algebraic closure, right?

We have that any polynomial in a field $K[x]$ factors into linear factors in the algebraic closure $\overline{K}[x]$. Does this hold also for the elements of a field of fraction $K(x)$?

Also how do we conclude that $\beta_i \in \mathbb{Q}$ ? (Wondering)