Proof that velocity of image by a plane mirror is negative of object

[Rhdjfgjgj]

Homework Statement

proof that velocity of image by a plane mirror is negative of object

Relevant Equations

V of image =-(v of object)

We were studying reflection due to plane mirrors and our sir derived the relation between velocity of image and velocity of object in case of a plane mirror. He took the following case as bare for deriving the formula.

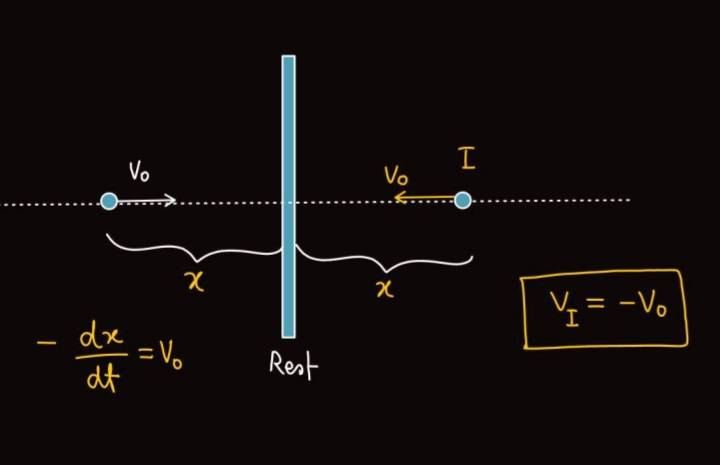
Following is the detailed working

Now I was wondering if I could derive it for a different case where the object is moving in opposite direction. But I'm not getting the same result. Look here please

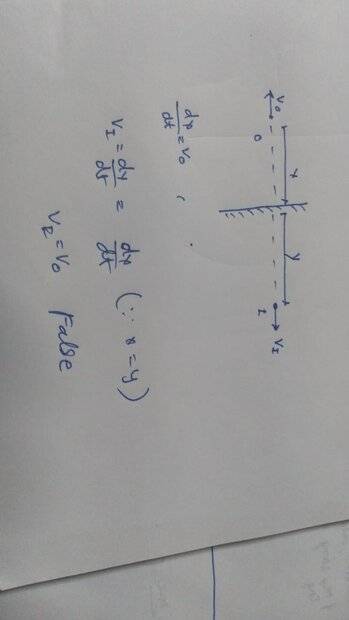
Why is it false this case . Or have I done something wrong. Please tell me where I'm wrong and the mathematical concept that I have to get right so that I don't repeat any of the mistakes again. Im sorry if the doubt was a bit to silly

 

[Mark44]

Your error is the same as in the first image you posted. That image shows $V_0$ on either side of the mirror, but one of them should be negative as the two are pointing in opposite directions.

Also, your work is very difficult to read, as the image appears rotated. At least the image is legible if I rotate my laptop's screen, which is more than I can say for some images that members post. In your work you wrote that $\frac{dx}{dt} = \frac{dy}{dt}$. This can't be true for the same reason as I gave above.

 

[Rhdjfgjgj]

Your error is the same as in the first image you posted. That image shows $V_0$ on either side of the mirror, but one of them should be negative as the two are pointing in opposite directions.

Also, your work is very difficult to read, as the image appears rotated. At least the image is legible if I rotate my laptop's screen, which is more than I can say for some images that members post. In your work you wrote that $\frac{dx}{dt} = \frac{dy}{dt}$. This can't be true for the same reason as I gave above.

Sorry about the images sir, . Back to the problem.
In the first image ,v of image was completely unknown , so I assumed it to be in same direction and found the actual velocity. But doing this way doesn't help me in the second case.Can u please do the steps for the second case

 

[Rhdjfgjgj]

Is this right

 

[Mark44]

In the first image ,v of image was completely unknown

In that image, there's no v. There are $V_0$ and $V_I$.

so I assumed it to be in same direction and found the actual velocity.

In the same direction as what?

But doing this way doesn't help me in the second case.

Can u please do the steps for the second case

No, we are not going to do the steps for you. In the second case, if the object is moving away from the mirror (at the same speed it was moving toward the mirror), its velocity will be the negative of what it was. That is $V_{new} = -V_0$.

 

[Mark44]

Is this right
View attachment 333792View attachment 333793

You are confusing yourself by introducing y in your equations. Instead of x and y, use x and -x. I'm assuming that the two points at the start of the arrows are equidistant from the mirror.