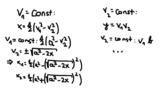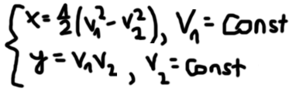Prove orthogonality of these curves

[berlinvic]

Homework Statement

Prove orthogonality of curves

Relevant Equations

Orthogonality condition for curves

I am asked to prove orthogonality of these curves, however my attempts are wrong and there's something I fundamentally misunderstand as I am unable to properly find the graphs (I have only found for a, but I doubt the validity).

Furthermore, I am familiar that to check for othogonality (based on the video ), I need to find both derivatives and make sure their multiplication is equal to -1. However, the introduction of constant a, b in my case doesn't help that at all and I am unable to check for orthogonality.

This has been bugging me for days, I would highly appreciate if someone could put me on the right path to solve this problem

 

[PeroK]

You've posted a 26-minute videos and some equations without much context. Please be more specific about what are your functions and how orthogonality is defined in this case.

Also, the homework guidelines require that you show us your best effort before we can help.

 

[berlinvic]

I think I posted everything that I've worked so far. The main equation for othogonality is the multiplication of derivatives of the curves equal to minus one, I mentioned it in the post as well. Additionally, I attached the photo where I show my work trying to parametrize the curves, but I'm stuck with curve y (not sure about the correctness of curve x). This is all I can think of, if you have any more inqueries I will try my best to provide more information.

 

[PeroK]

I think I posted everything that I've worked so far. The main equation for othogonality is the multiplication of derivatives of the curves equal to minus one, I mentioned it in the post as well. Additionally, I attached the photo where I show my work trying to parametrize the curves, but I'm stuck with curve y (not sure about the correctness of curve x). This is all I can think of, if you have any more inqueries I will try my best to provide more information.

Are the curves: $x^3 = 3(y -1)$ and $x(3y - 29) = 3$?

 

[berlinvic]

Are the curves: $x^3 = 3(y -1)$ and $x(3y - 29) = 3$?

No, sorry for confusion. In the picture I attached those are $x=\frac{1}{2}(v_1^2-v_2^2), v_1=const$ and $y=v_1v_2, v_2=const$

 

[PeroK]

No, sorry for confusion. In the picture I attached those are $x=\frac{1}{2}(v_1^2-v_2^2), v_1=const$ and $y=v_1v_2, v_2=const$

Aren't those surfaces? Above the $v_1, v_2$ plane?

 

[berlinvic]

Aren't those surfaces? Above the $v_1, v_2$ plane?

I don't think so based on that, v_1 and v_2 here are some constants not volumes.

 

[Mark44]

Thread closed.

@berlinvic, please start a new thread with a clear problem description. Not counting this post, we're up to 7 posts in this thread and the members here still don't know exactly what the question is asking. The video you posted, as already noted, is 26 minutes long. It is unreasonable for you to expect members to watch the whole video to understand what you need to do.
Also, the attachments you posted are virtually unreadable. When I attempted to expand them, the writing is black text against a very dark background, as if what you took a picture was very dimly lit. Many posts with photos of work are similarly difficult or impossible to read, and this is why we discourage including photos of the work.