Let's now prove the angle sum/difference identities for sine, cosine and tangent. First, we need to prove the law of cosines. I trust the reader will have available pencil and paper to make the drawings I describe. (Whew)
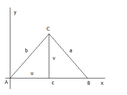
To begin, draw a horizontal line segment and label the left end $A$ and the right end $B$ and denote the length of the segment as $c$. Now place a point, labeled $C$ above the horizontal line, which is to the right of $A$ and to the left of $B$. Draw a line segment from $A$ to $C$ and label its length $b$ and draw a line segment from $B$ to $C$ and label its length $a$. We now have an acute triangle. Now, orient a Cartesian coordinate system such that vertex $A$ is at the origin, and segment $\overline{AB}$ lies on the $x$-axis. Next drop a vertical line from vertex $C$ to line segment $\overline{AB}$, dividing $\overline{AB}$ into two parts, the left which we label with the length $u$. The length of the vertical line we label $v$, as in the following sketch:
View attachment 949
Thus, the coordinates of the vertices are as follows:
$A=(0,0)$
$B=(c,0)$
$C=(u,v)$
Now, let angle $A$ denote the angle at vertex $A$, and the same with $B$ and $C$.
Thus, we have:
$$\cos(A)=\frac{u}{b}\,\therefore\,u=b\cos(A)$$
$$\sin(A)=\frac{v}{b}\,\therefore\,v=b\sin(A)$$
Thus, the coordinates of vertex $C$ are $(b\cos(A),b\sin(A))$. Now we can use the square of the distance formula to compute the distance from vertex $C$ to vertex $B$ (which is labeled $a$):
$$a^2=(b\cos(A)-c)^2+(b\sin(A)-0)^2$$
$$a^2=b^2\cos^2(A)-2bc\cos(A)+c^2+b^2\sin^2(A)$$
$$a^2=b^2\left(\sin^2(A)+\cos^2(A) \right)-2bc\cos(A)+c^2$$
$$a^2=b^2+c^2-2bc\cos(A)$$
I will leave it to the reader to verify this result when angle $A$ is obtuse. Now we are ready to prove the angle sum/difference identities for sine and cosine.
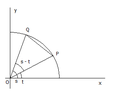
On the unit circle, place two points on the circle in quadrant 1, label the point closer to the $y$-axis $Q$ and the point closer to the $x$-axis $P$. Now draw three line segments, one from $O$ to $Q$, one from $O$ to $P$ and one from $P$ to $Q$. Label the angle subtended by the $x$-axis and segment $\overline{OP}$ as $t$ and the angle subtended by the $x$-axis and segment $\overline{OQ}$ as $s$. Thus, the angle subtended by segments $\overline{OP}$ and $\overline{OQ}$ is $s-t$. Refer to the following sketch:
View attachment 950
Now we will use two methods to compute the square of the distance from point $P$ to point $Q$. Using the law of cosines, we get:
$$\overline{PQ}^2=\overline{OP}^2+\overline{OQ}^2-2\cdot\overline{OP}\cdot\overline{OQ}\cos(s-t)$$
Because we are on the unit circle, $\overline{OP}=\overline{OQ}=1$, so we have:
$$\overline{PQ}^2=1^2+1^2-2\cdot1\cdot1\cos(s-t)$$
$$\overline{PQ}^2=2-2\cos(s-t)$$
Now, using the distance formula, we find that:
$$\overline{PQ}^2=(\cos(s)-\cos(t))^2+(\sin(s)-\sin(t))^2$$
$$\overline{PQ}^2=\cos^2(s)-2\cos(s)\cos(t)+\cos^2(t)+\sin^2(s)-2\sin(s)\sin(t)+\sin^2(t)$$
$$\overline{PQ}^2=\left(\cos^2(s)+\sin^2(s) \right)+\left(\cos^2(t)+\sin^2(t) \right)-2\cos(s)\cos(t)-2\sin(s)\sin(t)$$
$$\overline{PQ}^2=2-2\cos(s)\cos(t)-2\sin(s)\sin(t)$$
Now, equating the two expressions for $\overline{PQ}^2$, we obtain:
$$2-2\cos(s-t)=2-2\cos(s)\cos(t)-2\sin(s)\sin(t)$$
Subtract through by 2:
$$-2\cos(s-t)=-2\cos(s)\cos(t)-2\sin(s)\sin(t)$$
Divide through by -2:
$$\cos(s-t)=\cos(s)\cos(t)+\sin(s)\sin(t)$$
This is the angle-difference identity for cosine.
Now, we may write the left side as:
$$\cos(s+(-t))=\cos(s)\cos(t)+\sin(s)\sin(t)$$
Using the identities $\cos(-x)=\cos(x)$ and $\sin(-x)=-\sin(x)$ we have:
$$\cos(s+(-t))=\cos(s)\cos(-t)-\sin(s)\sin(-t)$$
Replacing $-t$ with $t$, we get:
$$\cos(s+t)=\cos(s)\cos()-\sin(s)\sin(t)$$
This is the angle-sum identity for cosine.
Now, for sine we can use the co-function identity $\sin(x)=\cos\left(\dfrac{\pi}{2}-x \right)$ which of course may be derived from what we have already found:
$$\sin(s+t)=\cos\left(\frac{\pi}{2}-(s+t) \right)=\cos\left(\left(\frac{\pi}{2}-s \right)-t \right)$$
Using the angle difference for cosine which we've already derived, we get:
$$\sin(s+t)=\cos\left(\frac{\pi}{2}-s \right)\cos(t)+\sin\left(\frac{\pi}{2}-s \right)\sin(t)$$
Using the co-function identities, this gives us:
$$\sin(s+t)=\sin(s)\cos(t)+\cos(s)\sin(t)$$
This is the angle-sum identity for sine.
Now, if we write the left side as:
$$\sin(s+(-t))=\sin(s)\cos(-t)+\cos(s)\sin(-t)$$
Applying the negative angle identities, we have:
$$\sin(s-t)=\sin(s)\cos(t)-\cos(s)\sin(t)$$
This is the angle-difference identity for sine.
Now, for the tangent function we can use $\tan(x)\equiv\dfrac{\sin(x)}{\cos(x)}$:
$$\tan(s+t)=\frac{\sin(s+t)}{\cos(s+t)}=\frac{\sin(s)\cos(t)+\cos(s)\sin(t)}{\cos(s)\cos(t)-\sin(s)\sin(t)}$$
Divide each term in the numerator and denominator by $\cos(s)\cos(t)$:
$$\tan(s+t)=\frac{\tan(s)+\tan(t)}{1-\tan(s)\tan(t)}$$
This is the angle-sum identity for tangent. For the angle-difference identity, we may write:
$$\tan(s-t)=\frac{\sin(s-t)}{\cos(s-t)}=\frac{\sin(s)\cos(t)-\cos(s)\sin(t)}{\cos(s)\cos(t)+\sin(s)\sin(t)}$$
Divide each term in the numerator and denominator by $\cos(s)\cos(t)$:
$$\tan(s-t)=\frac{\tan(s)-\tan(t)}{1+\tan(s)\tan(t)}$$
Thus, we have proven the following identities:
$$\sin(s\pm t)=\sin(s)\cos(t)\pm\cos(s)\sin(t)$$
$$\cos(s\pm t)=\cos(s)\cos(t)\mp\sin(s)\sin(t)$$
$$\tan(s\pm t)=\frac{\tan(s)\pm\tan(t)}{1\mp\tan(s)\tan(t)}$$