SUMMARY
The discussion centers on solving the arctan identity using the equation tan(a) + tan(b) + tan(c) = tan(a) * tan(b) * tan(c), where a + b + c = π. Participants explore the potential for utilizing the expressions for tan(a ± b) to simplify the problem. The conversation also touches on typesetting mathematical symbols, specifically the use of the π symbol. Ultimately, a geometric interpretation involving right triangles is presented as a solution.
PREREQUISITES
- Understanding of inverse trigonometric functions
- Familiarity with the tangent function and its properties
- Basic knowledge of trigonometric identities
- Ability to typeset mathematical equations using LaTeX
NEXT STEPS
- Study the derivation of the arctan identity in trigonometry
- Learn about the properties of the tangent function and its inverse
- Explore the use of the tan(a ± b) identities in solving trigonometric equations
- Review LaTeX typesetting for mathematical expressions
USEFUL FOR
Students and educators in mathematics, particularly those focusing on trigonometry and inverse functions, as well as anyone interested in enhancing their skills in typesetting mathematical equations.
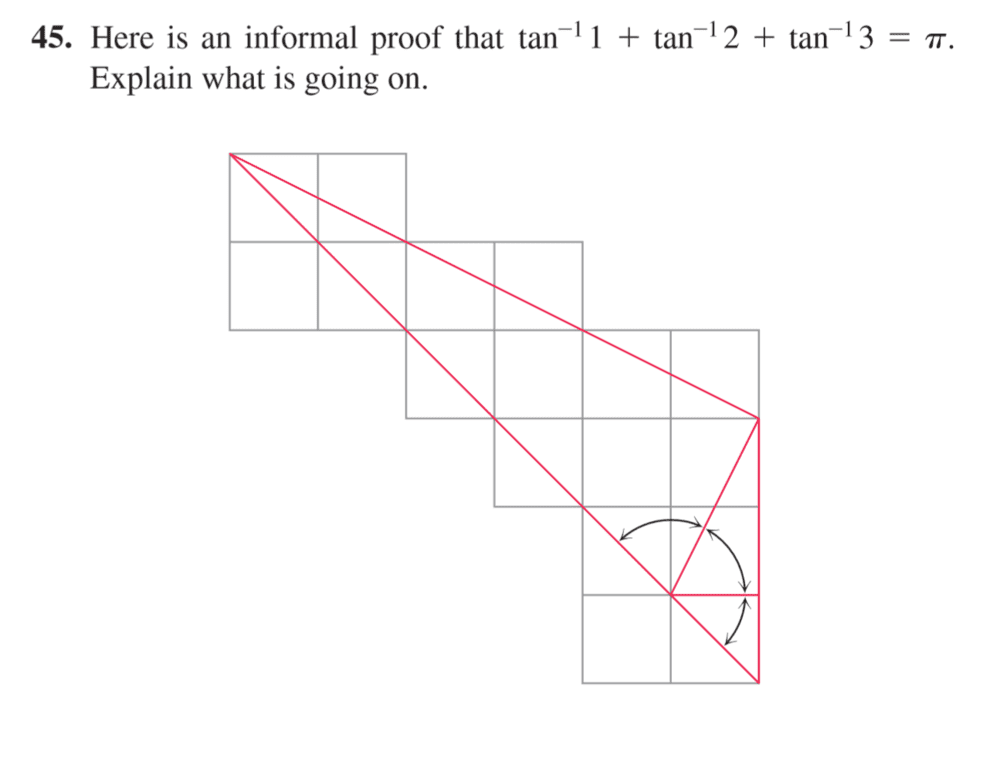
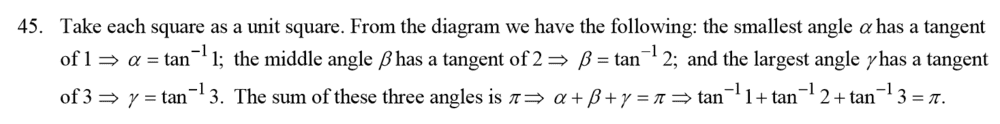
 ##\qquad## !
##\qquad## !