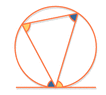
SUMMARY
The discussion centers on proving that angles CAB and CBA are equal in a triangle inscribed in a circle. The proof utilizes the inscribed angle theorem and the alternate segment theorem, establishing that the angles are equal due to their relationship with the arcs AC and CB. It concludes that triangle CBA is isosceles, as both angles CAB and CBA are equal, confirming the properties of angles in a circle.
PREREQUISITES
- Understanding of the inscribed angle theorem
- Familiarity with the alternate segment theorem
- Knowledge of basic properties of isosceles triangles
- Ability to interpret geometric diagrams involving circles and angles
NEXT STEPS
- Study the inscribed angle theorem in detail
- Explore the alternate segment theorem and its applications
- Practice problems involving isosceles triangles and their properties
- Learn about the relationships between angles and arcs in circle geometry
USEFUL FOR
Students of geometry, mathematics educators, and anyone interested in the properties of angles and triangles within circle geometry.