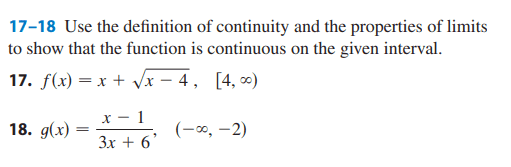SUMMARY
The discussion centers on the notation for expressing the continuity of the function g(x) over the interval (-∞, -2). Participants clarify that the notation "−∞ < a < −2" is equivalent to "a ∈ (-∞, -2)" and that including "For" in the expression is unnecessary. The consensus is that using "−∞ < a" does not provide additional information, as "a" is inherently a number and cannot equal negative infinity. The conversation emphasizes the importance of using proper mathematical notation to avoid confusion.
PREREQUISITES
- Understanding of mathematical notation and intervals
- Familiarity with concepts of continuity in functions
- Basic knowledge of inequalities
- Experience with interval notation
NEXT STEPS
- Research the properties of continuous functions in calculus
- Study the differences between interval notation and inequality notation
- Learn about the implications of including endpoints in interval notation
- Explore common mathematical notations used in textbooks
USEFUL FOR
Mathematics students, educators, and anyone interested in understanding proper mathematical notation and its implications in calculus and analysis.