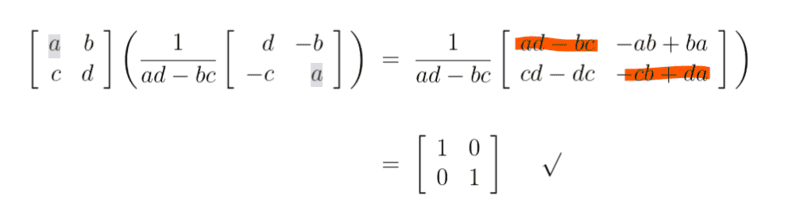SUMMARY
The discussion focuses on the formula for the inverse of a 2 x 2 matrix, specifically the expression $$\begin{pmatrix}a&b\\c&d\end{pmatrix}^{-1}=\begin{pmatrix}d&-b\\-c&a\end{pmatrix} \cdot (ad-bc)^{-1}$$. Participants clarify that the terms ##ad - bc## and ##-cb + da## are not equal to 1; rather, they are both divided by ##ad - bc## to yield 1. The procedure for calculating the inverse is emphasized as straightforward and useful for solving linear equations in two variables, as demonstrated through specific examples.
PREREQUISITES
- Understanding of matrix operations, specifically 2 x 2 matrices
- Familiarity with determinants in linear algebra
- Basic knowledge of linear equations and systems
- Proficiency in matrix multiplication
NEXT STEPS
- Study the properties of determinants in linear algebra
- Learn about matrix inversion techniques for larger matrices
- Explore applications of 2 x 2 matrix inverses in solving linear systems
- Investigate algorithms for matrix operations in programming languages like Python or MATLAB
USEFUL FOR
Students of linear algebra, mathematicians, and anyone interested in solving systems of linear equations using matrix methods.