Finding the eigenspace for this value of lambda

[ChiralSuperfields]

Homework Statement

Please see below

Relevant Equations

Please see below

For this,

I don't understand how they solved,

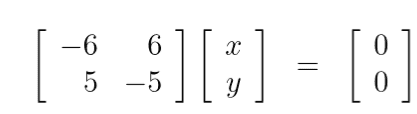
Because we would have to take the inverse of both side which would give the inverse of the matrix $2 \times 2$ matrix on the left hand side which dose not have an inverse.

Dose anybody please know how they did this?

Many thanks!

 

[FactChecker]

In equation form, we have $-6 x +6 y =0 \iff x - y = 0$ (dividing both sides by -6) for the first line. Likewise for the second line, $5 x -5 y =0 \iff x - y = 0$ (dividing both sides by 5). So both equations say the same thing.
Now you can see what they were doing in matrix form and why there is no need to include $x$ and $y$ where they were manipulating the augmented matrices. It really represents the same thing.

 

[DaveE]

There isn't a single solution for the eigenvector(s). That's why you can't invert that matrix. That's how it is with eigenvalue problems. In fact, that's how you find the eigenvalues with the characteristic equation |A-λI|=0, i.e. find λ that makes A-λI not invertable.

 

[Mark44]

Dose anybody please know how they did this?

Again, that's "does".

Your thread title indicates that you are to find the eigenspace for a matrix. IOW, the set of all nonzero vectors x (in $\mathbb R^2$ here) such that Ax = λx, or equivalently, $(A - \lambda I)\mathbf x = \mathbf 0$.
In order for x to be nonzero, the determinant of $A - \lambda I$ must be zero.

I'm guessing that your textbook is probably explaining this. Are you skipping over parts of the textbook?

 

[ChiralSuperfields]

Thank you @FactChecker , @DaveE and @Mark44!

I think I understand now :)

@Mark44, yes, sadly, I have to skip over parts of the textbook as the course jumps from one topic to another. Also sorry I did not see the dose again.