Proving Perpendicularity of Two Segments

[mathlearn]

Problem

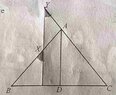
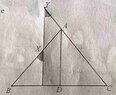
View attachment 6018

Workings

I was able to show that the triangles ABD & ACD are congruent as $AD$ is a common side and as $\angle BAC $ is bisected & $\angle ABC = \angle ACB$ give which makes them congruent by Angle Angle Side.

Where do I need help:

I am having trouble showing,

Show that $\angle XYA = \angle BXE$

View attachment 6020

& $\angle BEX = \angle BXE + \angle EBX$

 

[Euge]

Hi mathlearn,

Considering your first question, it's given that $AY$ and $AX$ are congruent, making triangle $XYA$ isosceles. What then can you say about $\angle XYA$ and $\angle AXY$? Also, what's the relationship between angles $\angle AXY$ and $\angle BXE$?

As for your second question, consider triangle $CYE$. The measure of exterior angle $\angle YEB$ is equal to the sum of the measures of remote interior angles $\angle CYE$ and $\angle ECY$: $\measuredangle YEB = \measuredangle CYE + \measuredangle ECY$. It's given that $\angle ABC\cong \angle ACB$, and by a previous part $\measuredangle XYA = \measuredangle BXE$. By substitution you'll get $\measuredangle BEX = \measuredangle BXE + \measuredangle EBX$.

 

[mathlearn]

Hi mathlearn,

Considering your first question, it's given that $AY$ and $AX$ are congruent, making triangle $XYA$ isosceles. What then can you say about $\angle XYA$ and $\angle AXY$? Also, what's the relationship between angles $\angle AXY$ and $\angle BXE$?

Bringing in the diagram again here,

View attachment 6021

$\angle XYA$ = $\angle AXY$ = $\angle BXE \left(\text{vertically opposite angles}\right)$

Hi mathlearn,

As for your second question, consider triangle $CYE$. The measure of exterior angle $\angle YEB$ is equal to the sum of the measures of remote interior angles $\angle CYE$ and $\angle ECY$: $\measuredangle YEB = \measuredangle CYE + \measuredangle ECY$. It's given that $\angle ABC\cong \angle ACB$, and by a previous part $\measuredangle XYA = \measuredangle BXE$. By substitution you'll get $\measuredangle BEX = \measuredangle BXE + \measuredangle EBX$.

Thank you very much (Nod)

For the third question as $\measuredangle ADC$ which is 90 = $\measuredangle XEB$ perpendicular drawn , therefore XE//AD

 

[mathlearn]

Bringing in the diagram again here,
$\angle XYA$ = $\angle AXY$ = $\angle BXE \left(\text{vertically opposite angles}\right)$
Thank you very much (Nod)

For the third question as $\measuredangle ADC$ which is 90 = $\measuredangle XEB$ perpendicular drawn , therefore XE//AD

I was just taking a look again at this problem and how can we say that $\measuredangle XEB$ = 90 degrees , I know that $\measuredangle XEB$ = 90 degrees but how can we prove that ? as nowhere in the problem mentions that line XE is a perpendicular drawn

$\measuredangle ADC$ can be proved 90 using triangle congruence

Many Thanks :)

 

[Euge]

Hi mathlearn,

It does turn out in this case that $\overline{XE}$ and $\overline{AD}$ are perpendicular to $\overline{BC}$, but by corresponding angles, to show that $\overline{XE}\,\|\, \overline{AD}$, it is enough to show that $m\measuredangle BXE = m\measuredangle BAD$. Let $\alpha = m\measuredangle XYA$ and $\beta= m\measuredangle XBE$. By the remote interior angles theorem $m\measuredangle XAY = m\measuredangle XBE + m\measuredangle ACB = \beta + \beta = 2\beta$. Since the sum of the measures of the interior angles of triangle $XAY$ (the measures are $\alpha, \alpha$, and $2\beta$) is $180^\circ$, then $2\alpha + 2\beta = 180^\circ$. Thus, looking to triangle $ABC$, we find $m\measuredangle BAC = 2\beta$. Since $\overline{AD}$ bisects $\measuredangle BAC$, $m\measuredangle BAD = \alpha$. We also know that $m\measuredangle BXE = \alpha$ from a previous exercise, so $m\measuredangle BAD = m\measuredangle BXE$, as desired.

Now, if you want to prove perpendicularity of $\overline{XE}$ and $\overline{AD}$ (and hence that $\overline{XE}\, \| \,\overline{AD}$), use the fact that $\alpha + \beta = 90^\circ$ (which follows from the equation $2\alpha + 2\beta = 180^\circ$ above). Since $\alpha = m\measuredangle BXE$, looking to triangle $BXE$ we find $m\measuredangle XEB = 90^\circ$; as $\alpha = m\measuredangle BAD$ (shown above), looking to triangle $BAD$ we find $m\measuredangle ADB = 90^\circ$. Hence, $\overline{XE}$ and $\overline{AD}$ are perpendicular to $\overline{BC}$.