Show that angle AXC=angle ACB; geometric construction

[mathlearn]

Looks like this question is going to make a long thread. :) This is what the problem states

Spoiler

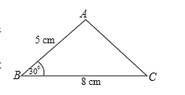
"Use only a straight edge with a cm/mm scale and a pair of compasses to do the following constructions. Draw your construction lines clearly.

View attachment 5914

(i) Construct the triangle ABC according to the measurements shown in the given sketch.

(ii) Construct a perpendicular from A to BC and name the point it meets BC as D.

(iii) Construct the circle that passes through the points A, C and D.

(iv) Construct the tangent to this circle at the point C, and name the point at which it meets AD produced as X.

(v) Show that $\angle$AXC = $\angle$ACB."

Using the pair of compass and a straight edge,

(i) Construct the triangle ABC according to the measurements shown in the given sketch.

Then,

(ii) Construct a perpendicular from A to BC and name the point it meets BC as D.

After That,

(iii) Construct the circle that passes through the points A, C and D.

Thereafter,

(iv) Construct the tangent to this circle at the point C, and name the point at which it meets AD produced as X.

Thereafter, The question states to mark the point where the tangent and AD produced as 'X'.Now can you help me to state, $\angle$AXC = $\angle$ACB. and I want to know verify the rest is done correctly. :) The updated diagram,

(v) Show that $\angle$AXC = $\angle$ACB.

Many thanks :)

 

[Evgeny.Makarov]

Now can you help me to state, $\angle AXC = \angle ACB$.

You have just stated it. Do you need to prove it? Note that a circumcircle around a right triangle has the hypotenuse as a diameter; therefore, $XC\perp AC$.

 

[mathlearn]

Yes the reasons must be given for the angles to be equal .Not getting It so far , An explanation with little detail would help :)

 

[Greg]

$$\angle{ACD}=90^\circ-\angle{CAD}$$

$$\angle{AXC}=\,?$$

 

[mathlearn]

$$\angle{ACD}=90^\circ-\angle{CAD}$$

$$\angle{AXC}=\,?$$

Hmm. True but the problem states To give reasons why $\angle AXC = \angle ACB$, not $\angle{ACD}$

As the given sketch looks a little bit difficult to refer, This sketch would help

View attachment 5917

This sketch looks easy to refer , and do you notice how $\angle AXC = \angle ACB$, in the sketch ; Now help me to state the reasons , please do your best to give a detailed reply really quick :)

 

[Evgeny.Makarov]

True but the problem states To give reasons why $\angle AXC = \angle ACB$, not $\angle{ACD}$

What's the difference?

You've been told that $\angle{ACD}=90^\circ-\angle{CAD}$. It is left to note that $\angle{AXC}=90^\circ-\angle{CAD}$ because $AC\perp CX$.

 

[mathlearn]

Hmm. True but the problem states To give reasons why $\angle AXC = \angle ACB$, not $\angle{ACD}$

My apologies, (Smile)

$$\angle{ACD}=90^\circ-\angle{CAD}$$

$$\angle{AXC}=\,?$$

You've been told that $\angle{ACD}=90^\circ-\angle{CAD}$. It is left to note that $\angle{AXC}=90^\circ-\angle{CAD}$ because $AC\perp CX$.

Oh! consider the two $$\triangle$$ ADC & $$\triangle$$ AXC

So that,

You've been told that $\angle{ACD}=90^\circ-\angle{CAD}$. It is left to note that $\angle{AXC}=90^\circ-\angle{CAD}$ because $AC\perp CX$.

View attachment 5918

Am I correct ? :) What theorem was used to gain this approach?

Many Thanks :)

 

[Evgeny.Makarov]

You have not written any reasoning except "Consider two triangles", so it's difficult to say whether you are correct.

Also please note that the forum rules prohibit asking for help in private messages.

 

[mathlearn]

Oh! I'm sorry (Doh)

You have not written any reasoning except "Consider two triangles", so it's difficult to say whether you are correct.

So considering the two triangles ADC & ACX,

$$\angle{ACD}=90^\circ-\angle{CAD}$$ & $$\angle{AXC}=90^\circ-\angle{CAD} $$

(v) Show that ∠AXC = ∠ACB.

$$\therefore$$ $$\angle{ACD}=\angle{AXC}$$

And Is there any theorem being used here?

Many Thanks (Smile)

 

[Evgeny.Makarov]

$$\angle{ACD}=90^\circ-\angle{CAD}$$ & $$\angle{AXC}=90^\circ-\angle{CAD} $$

$$\therefore$$ $$\angle{ACD}=\angle{AXC}$$

And Is there any theorem being used here?

Yes. The theorem that is used here says: For all numbers $x$, $y$ and $z$, if $x=z$ and $y=z$, then $x=y$. It's a basic property of equality.

 

[mathlearn]

I would like to thank both of you, :) Thanks :)

View attachment 5920