- #1
Hall
- 351
- 87
- Homework Statement
- Let S be a bounded nonempty subset of R such that sup S is not in S. Prove there is a sequence (sn) of points in S such that lim sn = sup S.
- Relevant Equations
- sup S is the least upper bound.
Let ##S=\{s_n:n∈N\}##. ##\sup S## is the least upper bound of S. For any ϵ>0, we have an m such that
##\sup S−\epsilon \lt s_m##
##\sup S−s_m \lt \varepsilon##
##|\sup S−s_m| \lt \varepsilon##
I mean to say that, no matter how small ϵ is, there is always an element of S whose distance from supS is less than that of ϵ, therefore there does exist a set of points which converge to supS, but I'm unable to get a thing like ##n \gt N \implies |\sup S−s_n| \lt \varepsilon##. Because, assume for a given ϵ, ##s_3## lies within ϵ of ##\sup S##, but ##s_4,s_5⋯s_n## all lies beyond the coverage of ##\epsilon##
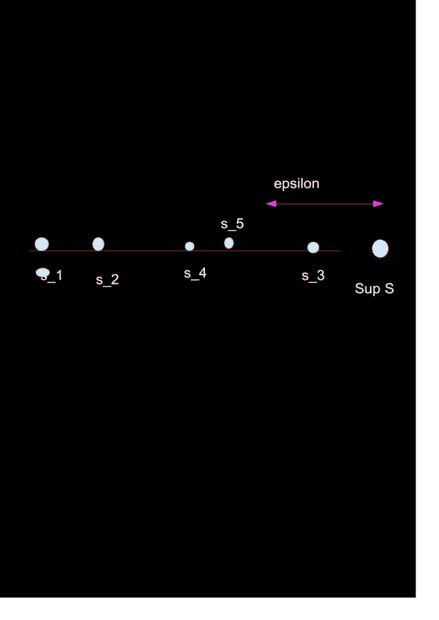
##\sup S−\epsilon \lt s_m##
##\sup S−s_m \lt \varepsilon##
##|\sup S−s_m| \lt \varepsilon##
I mean to say that, no matter how small ϵ is, there is always an element of S whose distance from supS is less than that of ϵ, therefore there does exist a set of points which converge to supS, but I'm unable to get a thing like ##n \gt N \implies |\sup S−s_n| \lt \varepsilon##. Because, assume for a given ϵ, ##s_3## lies within ϵ of ##\sup S##, but ##s_4,s_5⋯s_n## all lies beyond the coverage of ##\epsilon##